Altitude of a Triangle
Altitude of a Triangle: Overview
This topic covers concepts, such as, Altitude of Triangles, Basic Properties of Altitudes of Triangles & Altitudes and Medians in Equilateral Triangles etc.
Important Questions on Altitude of a Triangle
A triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is , then the altitude of the triangle is?
In , , the altitude to the base divides vertex angle into two parts and adjacent to , then which one of the relation can be obtained?
Let be an equilateral triangle and , , be the altitudes. Then the right statement out of the four given responses is:
In triangle is the altitude to . Which of the following must be true?
The number of altitudes of a triangle is
If the length of the sides of a triangle are cm, cm and cm. Then find the length of the altitude drawn on side having length cm.
In a right angle triangle PQR right-angled at Q. If the length of PQ and QR are respectively cm and cm, then find the length of altitude QT drawn on PR?
If the length of the two altitudes of a are and , then what would be the possible length of the unknown altitude?
In and is perpendicular to at . In and is perpendicular to at . If , then is equal to:
Name the orthocentre of .
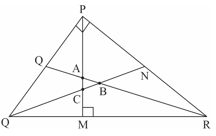
Identify the type of segment required in the below triangle:
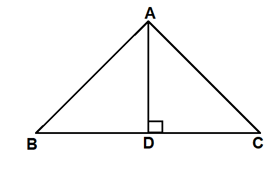
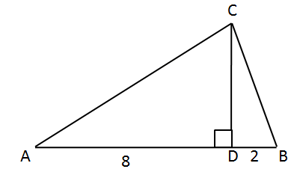
is a right angled triangle. If then find .
If the altitude to side of triangle with side is then find .
Given: is the altitude, . If then find .
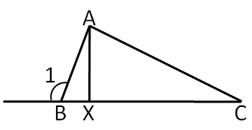
Given: is the altitude, . If is then find
The corresponding sides of two similar triangle are in the ratio , then the ratio of their altitude will be:
and are medians of right-angled at and .If . Find the length of .
Where does the orthocentre lie in the case of a right angled triangle?
Where does the orthocentre lie in the case of an obtuse-angled triangle?
Where does the orthocentre lie in the case of an acute-angled triangle?
