Inequalities in a Triangle
Inequalities in a Triangle: Overview
This topic covers concepts such as Inequalities in a Triangle, Side Opposite to Larger Angle in a Triangle, Side Opposite to Smaller Angle in a Triangle, Triangle Inequality for Sum of Sides, and Triangle Inequality for Difference of Sides.
Important Questions on Inequalities in a Triangle
is a median of the triangle . If then find .
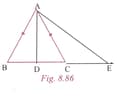
ABC is an isosceles triangle with AB = AC. D is any point online segment BC and E is a point on BC produced.
Prove that : AE > AD
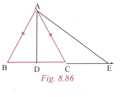
is an isosceles triangle with is any point online segment and is a point on produced.
Prove that :
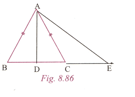
is an isosceles triangle with . is any point on line segment and is a point on produced.
Prove that:
Prove that in a triangle, other than equilateral triangle, the angle opposite to the longest side is greater than of a right angle.
In a PQR, PS is drawn perpendicular to QR. If SR > QS, Show that PR > PQ.
If O is any point in the exterior of ABC, show that (AB+BC+AC)< (OA+OB+OC)
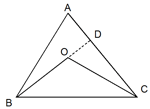
ABC is a triangle and O is any point inside the triangle. Show that OB + OC < AB + AC
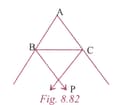
In Figure , the sides and of are produced and the bisectors of external angles and meet at . If
, Prove that .
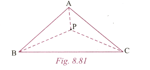
In Figure, is any point inside the triangle . Prove that .
Can you draw a triangle with sides , and ?
Can you draw a triangle with sides and ?
Can you draw a triangle with sides and ?
Can you draw a triangle with sides and ?
is a quadrilateral. is any point inside the quadrilateral. Prove that .
A student has proposed triangles with the following dimensions:
i) 4 cm, 8 cm, 3 cm
ii)1000 meter, 1500 meter, 500 meter
iii) 2 km, 3km, 10 km
iv)1mm, 3mm, 3mm
Find which one of his proposals is correct.
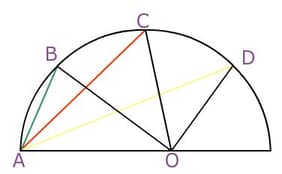
Shown below are some triangles Salim constructed,△OAB, △OAC, and △OAD
Now he wants to construct one more triangle OAE, such that OA + OE = AE. He marks point E on the circle and joined E with points A and O.
Which of the following constructions could he have made?
In a triangle , median intersect at point prove that:
Two sides of a triangle are of lengths and . The length of the third side cannot be more than or equal to . Find the value of .
In , . Without finding the angles of the triangles, name its smallest side in alphabetical order.