Sum of the Measures of the Exterior Angles of a Polygon

In a quadrilateral $ABCD$, the angles $A, B, C$ and $D$ are in ratio $3:5:9:13$. Find the measure of each angles of the quadrilateral.

In a quadrilateral $ABCD$, the angles $A, B, C$ and $D$ are in ratio $1:2:4:5$. Find the measure of each angles of the quadrilateral.

Three angles of quadrilateral are respectively equal to $110°, 50°$ and $40°$. Find its fourth angle.

In a quadrilateral $ABCD$, the angles $A, B, C$ and $D$ are in ratio $1:2:3:4$. Find the measure of each angles of the quadrilateral.

The angle of a quadrilateral are respectively $100°, 98°, 92°$ . Find the fourth angle.

$K°$ is the maximum exterior angle possible for a regular polygon, then find the value of $k$.

Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

Figure
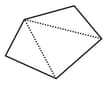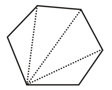Side	$3$	$4$	$5$	$6$
Angle	$180°$	$2\times 180°$ $=(4-2)\times 180°$	$3\times 180°$ $=(5-2)\times 180°$	$4\times 180°$ $=(6-2)\times 180°$

The angles of a quadrilateral are $ {x°}$, $ {(x-20)}^{°}$, $ {(x-30)}^{°}$, and $ 2{x°}$. What is the value of the greatest angle?

The two angles of a quadrilateral are equal to $ 78°$ and $ 142°$ and the other two angles are equal. The measure of the equal angles are

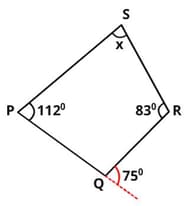
What is the value of ∠$ S$ ?

ABCD and PQRS are 2 quadrilaterals. Choose the correct statement from the following.

The sum of the angles of a quadrilateral is

The sum of the angles of a quadrilateral is equal to the sum of

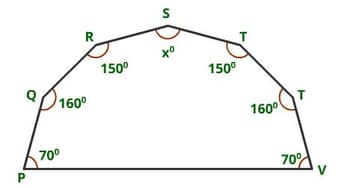
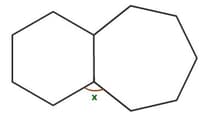
An outline of a camping tent is shown below. The value of $ x$ is_____ degrees.

The value of x is_____ degrees.

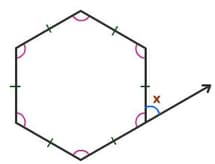
Two regular polygons are joined as shown below, The value of x is_____ degrees.

(Round your answer to the nearest degree.)

The border of a coin is in the shape of regular polygon. The measure of each interior angle of the border is_____ degrees.

(Round your answer to the nearest degree.)

Find the sum of the interior angle measures of a 13-gon.

Ram and Shyam solve the above question in their unit test. The solutions they write are given below. Which solution is correct?