Number of Edges, Faces and Vertices of Polyhedrons
Number of Edges, Faces and Vertices of Polyhedrons: Overview
This topic unfolds the concept of number of faces, edges and vertices of polyhedron. Through a table, we will understand the number of faces, edges and vertices of a cube, cuboid, pentagonal prism and pyramid, tetrahedron etc.
Important Questions on Number of Edges, Faces and Vertices of Polyhedrons
Icosahedron has 20 faces and 30 edges. The number of vertices for the icosahedron will be _____
What will be the number of faces, edges and vertices of a pyramid whose base is a polygon of N sides ?
Can a simple solid have 6 edges and 7 vertices? Verify using Euler’s formula.
What will the number of faces be for a structure of a molecule which has 60 carbon atoms that are joined together by 90 bonds?

The following image satisfies Euler’s formula.
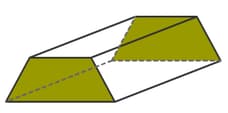
If this is cut by a horizontal plane, then will the lower portion of the cut solid (frustum) satisfy the Euler’s formula?
What is the name of the polyhedron with 10 faces and 16 vertices?
The solid shown below does not satisfy the Euler’s formula as that solid is a concave polyhedron. How can you cut the solid in such a way that both the cut pieces satisfy the Euler’s formula.

Is there any simple regular polyhedron that has exactly ten faces and seventeen vertices?
Euler’s formula can be applied to all the polyhedrons. Is this statement correct?
Identify the solid that does not satisfy the Euler’s formula.
The value of the Euler’s formula, F+V-E for a cube is _____.
Can a polyhedron have faces, edges and vertices?
Verify Euler's formula for the following solid (show calculations).
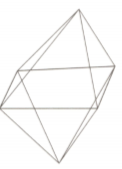
Verify Euler's formula for the following solid (show calculations).
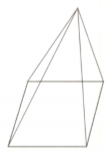
The number of edges and vertices in a solid are and , respectively. The number of faces are
To find the missing number of vertex, face or edge of a solid using Euler's formula.
Verify Euler's Formula for the following.
Triangular pyramid
