The Mid-point Theorem

$ABC$ is an isosceles right-angled triangle in which $\angle A=90°$. A straight line parallel to $BC$ intersects $AB \text{and} AC \text{at} D \text{and} E$ respectively. If the value of $\angle ADE=x°$, then find the value of $x$.

$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a quadrilateral in which $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ and $\mathrm{S}$ are mid-points of the sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}, \mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$. $\mathrm{A}\mathrm{C}$ is a diagonal. Then, $\mathrm{S}\mathrm{R}\parallel \mathrm{A}\mathrm{C}$ and $\mathrm{S}\mathrm{R}=\frac{1}{2}\mathrm{A}\mathrm{C}$
 

Let $AD$ and $BC$ be the parallel sides of a trapezium $ABCD.$ Let $P$ and $Q$ be the midpoints of the diagonals $AC$ and $BD.$ If $AD=16$ and $BC=20,$ then what is the length of $PQ ?$

In $∆\mathrm{ABC}, \mathrm{E}$ is the mid-point of median $\mathrm{AD}$ such that $\mathrm{BE}$ produced meets $\mathrm{AC}$ at $\mathrm{F}$. If $\mathrm{AC}=10.5 \mathrm{cm}$, then $\mathrm{AF}=3.5 \mathrm{cm}$.

If $D$ and $E$ are respectively the midpoints of the sides $AB$ and $BC$ of $∆ABC$ in which $AB=7.2 \mathrm{cm}, BC=9.8 \mathrm{cm}$ and $AC=3.6 \mathrm{cm}$ then determine the length of $DE$.

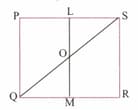
In Figure shown below, PQRS is a square. L and M are respectively, the mid points of PS and QR. Find the area of $△OLS$, if $PQ=$ $8$ cm, and O is the point of intersection of LM and QS.

In a $△\mathrm{LMN},$$\mathrm{A}$ and$\mathrm{B}$  are mid points of $\mathrm{LM}$ and $\mathrm{MN}$ respectively. Calculate $\angle \mathrm{ABM} \mathrm{if} \angle \mathrm{LNM} = {45}^0$

In a $△\mathrm{LMN},$$\mathrm{A}$ and $\mathrm{B}$ are mid points of $\mathrm{LM}$ and$\mathrm{MN}$ respectively. Calculate $\mathrm{AB} \mathrm{if} \mathrm{LN}=8 \mathrm{cm} .$

In a $△\mathrm{PQR}, \mathrm{L} \mathrm{and} \mathrm{N}$ are mid points of sides $\mathrm{PQ}$ and $\mathrm{PR}$ respectively. If $\mathrm{LN}=3$ cm then what is the length of $\mathrm{QR}$?

Prove that the triangle formed by joining the mid points of the sides of an isosceles triangle is also an isosceles triangle. 

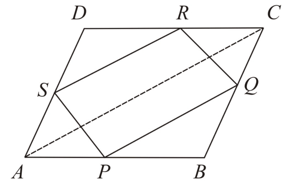
In given figure, $L$and $T$ are respectively the mid-points of the opposite sides $PQ$and $SR$of a parallelogram $PQRS$. $SL$ and $TQ$intersect $PR$ at $M$ and $N$respectively. Show that$PM = MN = NR$.

ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that area (DCYX) = $\frac{7}{9}$ area (XYBA).

ABC is a triangle whose area is $50 {\mathrm{cm}}^2$. $E$ and $F$ are mid points of the sides $AB$ and $AC$ respectively. Prove that $EBCF$ is a trapezium. Also find its area.

Show that the quadrilateral formed by joining the mid points of the adjacent sides of a square is also a square.

In a rectangle ABCD, prove that  $A{C}^2+B{D}^2=A{B}^2+B{C}^2+C{D}^2+D{A}^2.$

In any triangle ABC, prove that three times the sum of squares of its sides is equal to four times the sum of squares of its medians.

Show that the quadrilateral, formed by joining the mid-points of the consecutive sides of a rhombus is a rectangle.

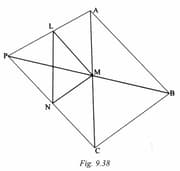
In Fig. $9.38,$ from a point $\mathrm{P}$, straight lines $\mathrm{PA}, \mathrm{PB} \mathrm{and} \mathrm{PC}$ of unequal lengths are, drawn. If $\mathrm{L}, \mathrm{M} \mathrm{and} \mathrm{N}$ are their mid points respectively, prove that $△\mathrm{ABC} \mathrm{and} △\mathrm{LMN}$ are equiangular.

In a right angled triangle $\mathrm{ABC},\angle \mathrm{ABC}={90}^0$ and $\mathrm{D}$ is mid point of $\mathrm{AC}$. Prove that $\mathrm{BD}=\frac{1}{2}\mathrm{AC}.$

 

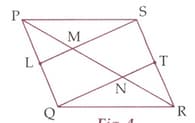
In a kite shaped figure $\mathrm{ABCD}, \mathrm{AB}=\mathrm{AD} \mathrm{and} \mathrm{BC}=\mathrm{CD}.$ Points $\mathrm{P}, \mathrm{Q} \mathrm{and} \mathrm{R}$ are mid points of sides $\mathrm{AB}, \mathrm{BC} \mathrm{and} \mathrm{DC}$ respectively. Prove that

line through $\mathrm{P}$ and parallel to $\mathrm{QR}$ bisects side $\mathrm{AD}.$