The Work-Energy Principle

A box of mass $5 \mathrm{kg}$ is pushed $5 \mathrm{m}$ up a slope inclined at $30°$ to the horizontal by a force of $30 \mathrm{N}$ parallel to the slope. The frictional force acting on the box is $3 \mathrm{N}$. Find the work done against gravity. (Use: $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)

A box of mass $5 \mathrm{kg}$ is pushed $5 \mathrm{m}$ up a slope inclined at $30°$ to the horizontal by a force of $30 \mathrm{N}$ parallel to the slope. The frictional force acting on the box is $3 \mathrm{N}$.

Find the work done against friction.

A box of mass $5 \mathrm{kg}$ is pushed $5 \mathrm{m}$ up a slope inclined at $30°$ to the horizontal by a force of $30 \mathrm{N}$ parallel to the slope. The frictional force acting on the box is $3 \mathrm{N}$. Find the work done by the push force.

A box of mass $5 \mathrm{kg}$ is pushed up a slope. The box has initial speed $2{ \mathrm{ms}}^{-1}$ and final speed $3 \mathrm{m}{ \mathrm{s}}^{-1}$. Find the increase in the kinetic energy of the box.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

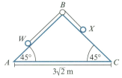
Explain why the work done by the tension does not need to be included in the work-energy calculation.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

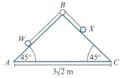
Use the work-energy principle to find the speed of the particles when particle $X$ reaches the ground at $C$.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

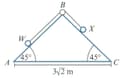
Find the change in the total potential energy when particle $X$ moves a distance $x \mathrm{m}$.

Particle $W$, of mass $3 \mathrm{kg}$, and particle $X$, of mass $5 \mathrm{kg}$, are attached to the ends of a light, inextensible string of length $4 \mathrm{m}$. The string passes over a small smooth pulley fixed at the top of a fixed triangular wedge, $ABC$. The angles $BAC$ and $BCA$ are each $45°$ and the side $AC$ is fixed to horizontal ground. The distance from $A$ to $C$ is $3\sqrt{2} \mathrm{m}$. Surface $AB$ is smooth and surface $BC$ is rough, with coefficient of friction $\frac{1}{\sqrt{8}}$ Particle $W$ is held at the bottom of the slope $AB$ and is then gently released.

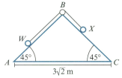
Find the work done against friction when particle $X$ moves a distance $x \mathrm{m}$.

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Show that $21v^2=220x$.

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Find, in terms of $x$,

the work done against the frictional force.

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Find, in terms of $x$,

the loss of gravitational potential energy of the system,

A light inextensible rope has a block $A$ of mass $5 \mathrm{kg}$ attached at one end, and a block $B$ of mass $16 \mathrm{kg}$ attached at the other end. The rope passes over a smooth pulley which is fixed at the top of a rough plane inclined at an angle of $30°$ to the horizontal. Block $A$ is held at rest at the bottom of the plane and block $B$ hangs below the pulley (see diagram). The coefficient of friction between $A$ and the plane is $\frac{1}{\sqrt{3}}$. Block $A$ is released from rest and the system starts to move. When each of the blocks has moved a distance of $x \mathrm{m}$ each has speed $v \mathrm{m}{ \mathrm{s}}^{-1}$.

Write down the gain in kinetic energy of the system in terms of $v$.

A block of mass $25 \mathrm{kg}$ is dragged across a rough horizontal floor, using a rope that makes an angle of $30°$ with the floor. The coefficient of friction between the floor and the block is $0.25$. The tension in the rope is $T \mathrm{N}$ and air resistance can be ignored. After travelling a distance of $5 \mathrm{m}$, the speed of the box has increased by $2 \mathrm{m}{ \mathrm{s}}^{-1}$.

Use the work-energy principle to find, in terms of $T$, the average of the initial and final speeds.

A block of mass $25 \mathrm{kg}$ is dragged across a rough horizontal floor, using a rope that makes an angle of $30°$ with the floor. The coefficient of friction between the floor and the block is $0.25$. The tension in the rope is $T \mathrm{N}$ and air resistance can be ignored. After travelling a distance of $5 \mathrm{m}$, the speed of the box has increased by $2 \mathrm{m}{ \mathrm{s}}^{-1}$.

Find the work done against friction, in terms of $T$.

A lorry of mass $14000 \mathrm{kg}$ moves along a road starting from rest at a point $O$. It reaches a point $A$, and then continues to a point $B$ which it reaches with a speed of $24 \mathrm{m}{ \mathrm{s}}^{-1}$. The part $OA$ of the road is straight and horizontal and has length $400 \mathrm{m}$. The part $AB$ of the road is straight and is inclined downwards at an angle of $\theta °$ to the horizontal and has length $300 \mathrm{m}$.

Find the value of $\theta$.

A lorry of mass $14000 \mathrm{kg}$ moves along a road starting from rest at a point $O$. It reaches a point $A$, and then continues to a point $B$ which it reaches with a speed of $24 \mathrm{m}{ \mathrm{s}}^{-1}$. The part $OA$ of the road is straight and horizontal and has length $400 \mathrm{m}$. The part $AB$ of the road is straight and is inclined downwards at an angle of $\theta °$ to the horizontal and has length $300 \mathrm{m}$.

i For the motion from $O$ to $B$, find the gain in kinetic energy of the lorry and express its loss in potential energy in terms of $\theta$. The resistance to the motion of the lorry is $4800 \mathrm{N}$ and the work done by the driving force of the lorry from $O$ to $B$ is $5000 \mathrm{kJ}$.

A car of mass $1200 \mathrm{kg}$ is driven along a straight horizontal road against a resistance of $5000 \mathrm{N}$. The engine has a maximum power output of $100 \mathrm{kW}$.

Find the maximum speed the car can reach.

A car of mass $1000 \mathrm{kg}$ travels in a straight line up a slope inclined at angle $\alpha$ to the horizontal, where $\sin \alpha =0.05$. The non-gravitational resistances are $200 \mathrm{N}$ throughout the motion.

When the power produced by the engine is $50 \mathrm{kW}$, the car is accelerating at $1.2 \mathrm{m}{ \mathrm{s}}^{-2}$.  What would happen to the speed if the mass of the car increased?

A car of mass $1000 \mathrm{kg}$ travels in a straight line up a slope inclined at angle $\alpha$ to the horizontal, where $\sin \alpha =0.05$. The non-gravitational resistances are $200 \mathrm{N}$ throughout the motion.

When the power produced by the engine is $50 \mathrm{kW}$, the car is accelerating at $1.2 \mathrm{m}{ \mathrm{s}}^{-2}$. Find the speed of the car at this instant.

A van of mass $1500 \mathrm{kg}$ starts from rest. It is driven in a straight line up a slope inclined at angle $\alpha$ to the horizontal, where $\sin \alpha =\frac{1}{10}$. The driving force of the engine is $2000 \mathrm{N}$ and the non-gravitational resistances total $350 \mathrm{N}$ throughout the motion. The speed of the van is $v \mathrm{m}{ \mathrm{s}}^{-1}$ when it has travelled $x \mathrm{m}$ from the start. Use the work-energy principle to find $v$ in terms of $x$.(Use: $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)