Area of a Triangle

The Class $\mathrm{X}$ students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of $1 \mathrm{m}$ from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

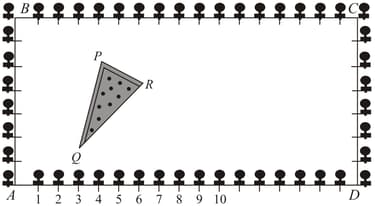
Taking $A$ as origin, find the coordinates of the vertices of the triangle. What will be the coordinates of the vertices of $∆PQR$ if $C$ is the origin? If the area of triangles in both the cases is $k \mathrm{square} \mathrm{units}$, then find the value of $k$. 

Find the value of $\mathrm{}\mathrm{‘}k\mathrm{’}$, for which the points are collinear.
 $\left(7,-2\right), \left(5,1\right), \left(3,k\right)$

Find the area of the triangle whose vertices are $\left(-5,-1\right), \left(3,-5\right), \left(5,2\right)$.

The vertices of a $\mathrm{}∆\mathrm{A}\mathrm{B}\mathrm{C}$ are $\mathrm{}\mathrm{A}\left(4,\mathrm{}6\right)$, $\mathrm{}\mathrm{B}\left(1,\mathrm{}5\right)$ and $\mathrm{}\mathrm{C}\left(7,\mathrm{}2\right)$. A line is drawn to intersect sides $\mathrm{}\mathrm{A}\mathrm{B}$ and $\mathrm{}\mathrm{A}\mathrm{C}$ at $\mathrm{D}\mathrm{}$and $\mathrm{}\mathrm{E}$ respectively, such that $\frac{\mathrm{A}\mathrm{D}}{\mathrm{A}\mathrm{B}}=\frac{\mathrm{A}\mathrm{E}}{\mathrm{A}\mathrm{C}}=\frac{1}{4}$. Calculate the area of the $\mathrm{}∆\mathrm{A}\mathrm{D}\mathrm{E}$ and compare it with the area of $\mathrm{}∆\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$.

The Class $\mathrm{X}$ students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of $1 \mathrm{m}$ from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

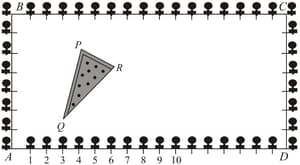
Taking $\mathrm{}\mathrm{A}$ as origin, find the coordinates of the vertices of the triangle.

Find a relation between $x$and $y$ if the points $\left(x,y\right), \left(1,2\right)$ and $\left(7,\mathrm{}0\right)$ are collinear.

 The median of a triangle divides it into two triangles of equal areas. Verify this result for $\mathrm{}∆\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$ whose vertices are $\mathrm{A}\left(4,-6\right), \mathrm{B}\left(3,-2\right)$ and $\mathrm{}\mathrm{C}\left(5,\mathrm{}2\right)$

Find the area of the quadrilateral whose vertices, taken in order, are $\left(-4,-2\right), \left(-3,-5\right), \left(3,-2\right)$ and $\left(2,\mathrm{}3\right)$.

Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are $\left(0,-1\right), \left(2,1\right)$ and $\left(0,\mathrm{}3\right)$. Find the ratio of this area to the area of the given triangle.

In each of the following find the value of $\mathrm{}\mathrm{‘}k\mathrm{’}$, for which the points are collinear.
 $\left(8,1\right), \left(k,-4\right), \left(2,-5\right)$
 

Find the area of the triangle whose vertices are:
 $\left(2,3\right),\left(-1,0\right),\left(2,-4\right)$