Distance Formula
Distance Formula: Overview
This topic explains how to find the distance between two points, if the coordinates of both the points are given. We will also derive the Distance formula in a step-by-step manner.
Important Questions on Distance Formula
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
Find the distance between the following pair of points.
Find the distance between the pair of points:
is a rectangle formed by the points and . and are the midpoints of and respectively. Is the quadrilateral a square? A rectangle? Or a rhombus? Justify your answer.
Find the centre of a circle passing through the points and .
Find the area of a rhombus if its vertices are and taken in order.
[Hint: Area of a rhombus (product of its diagonals)]
Find a relation between and such that the point is equidistant from the point and .
If is equidistant from and , find the values of . Also find the distances and .
Find the values of for which the distance between the points and is units.
Find the point on the axis which is equidistant from and .
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
In a classroom, friends are seated at the points and as shown in Fig. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think is a square?” Chameli disagrees.
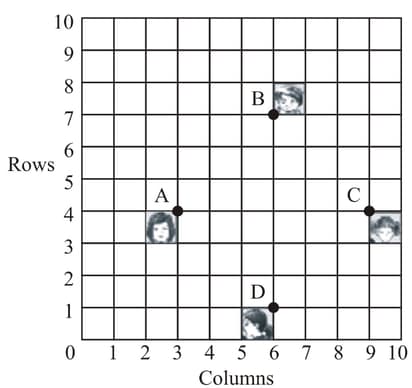
Using distance formula, find which of them is correct.
Check whether and are the vertices of an isosceles triangle.
Determine if the points and are collinear.
Find the distance between the points and .
Find the distance between the following pairs of points:
