Distance Formula

Find the point on $y\text{-axis}$ which is equidistant from the points $\left(5,-2\right)$ and $\left(-3,2\right)$.

Triangle $ABC$ has vertices $A(3,-1), B(-3,-5)$ and $C(-1,5)$. Determine whether the triangle is a right triangle. Fully justify your answer.

Show that the points $\left(p, p\right), \left(-p, -p\right), \left(p\sqrt{3}, -p\sqrt{3}\right)$ are vertices of an equilateral triangle.

Show that the points $A\left(2, 7\right), B\left(3, 0\right), C\left(-4, -1\right)$ are vertices of an isosceles triangle and find the length of base.

$A\left(2, 0\right), B\left(4, 4\right)$ and $C\left(6, 2\right)$ are the vertices of $∆ABC$. The mid-points of $\overline{BC}, \overline{CA}$ and $\overline{AB}$ are $D\left(5, 3\right), E\left(4, 1\right)$ and $F\left(3, 2\right)$ respectively. Then find the length of three medians.

Prove that the coordinates of $A$ and $B$ be $\left(3, 2\right)$ and $\left(-6, -4\right)$ respectively, then the line $AB$ passes through the origin.

Show that the points $\left(2a, 6a\right), \left(2a, 4a\right)$ and $\left(2a+\sqrt{3}a, 5a\right)$ are the vertices of an equilateral triangle of side $2a$ units.

Calculate the distance between the following pair of point.

$\left(5,8\right)$ and $\left(5,-3\right)$

A circle of radius $10$ is drawn with the origin as centre. Check whether each of the points with coordinates $(6, 9), (5, 9), (6, 8)$ is inside, outside or on the circle.

Prove that by joining the points $(2, 1), (3, 4), (-3, 6)$ we get a right triangle.

Prove that the points $(1,3), (2,5)$ and $\left(3, 5\right)$ are on the same line.

Find the distance between the following pair of points
$(7, 8)$ and $(-2, 3)$

Two points $P$ and $Q$ have the coordinates $\left(3,2\right)$ and $\left(7,6\right)$, respectively. Find the equation of perpendicular bisector of $PQ$.

Write down the coordinates of the point $P$, that divides the line joining$A (2,1)$ and $B(-7,10)$  in the ratio $2:1$.Calculate the distance $OP$, where $O$ is the origin.

In the given figure, $ABC$ is a triangle and $BC$ is parallel to $Y-\mathrm{axis}$. $AB$ and  $AC$ intersect the $Y-\mathrm{axis}$ at $P$ and $Q$, respectively.

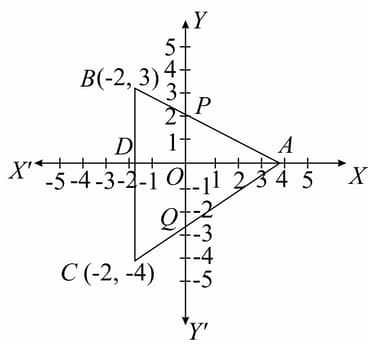
Find the length of $AB \mathrm{and} AC$.

Triangle having vertices $(-2, 1), (2, -2)$ and $(5, 2)$ is a/an

The distance between the two points $(2,3)$ and $(1,4)$ is

$AOBC$ is rectangle whose three vertices are $A(0, 3), O(0, 0)$ and $B(5, 0)$. The length of its diagonal is

The points $(-4, 0), (4, 0), (0, 3)$ are the vertices of a

The distance of the point $P(-6, 8)$ from the origin is