Trigonometric Ratios

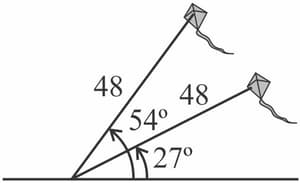
A kite string is $48 \mathrm{m}$ long. As the wind blew, the angle between the kite and the ground went from $27$ degrees to $54$ degrees. Determine the increase in the vertical height of the kite above the ground.

Identify "Hypotenuse", "opposite side", and "Adjacent side" for the angle $X$ in the given triangle.

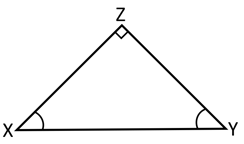
In a right angle triangle $ABC$ right angle is at $C. BC+CA=23 \mathrm{cm}$ and $\mathrm{BC}-\mathrm{CA}=7 \mathrm{cm}$, then find $\sin A$ and $\sin B$.

If in a right angled triangle $ABC,\angle B$ is a right angle; then find the value of $\sin A,\cos C$ and $\tan A$.

Given $AC=5 \mathrm{cm},AB=3 \mathrm{cm},BC=4 \mathrm{cm}$.

One of the trigonometric ratio is given as $\mathrm{tan\theta }=\frac{3}{4}$, find the remaining trigonometric ratios.

In the following figure how will you find the trigonometric ratios for $\angle XYZ=q$?

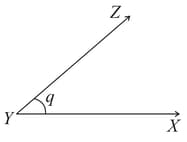
 In a $△\mathrm{ABC}$, $\mathrm{AD}$ is the bisector of $\angle \mathrm{BAC}$ . If $\mathrm{AB}=8 \mathrm{cm}$, $\mathrm{BD}=6 \mathrm{cm}$ and $\mathrm{DC}=3 \mathrm{cm}$. The length of the side $\mathrm{AC}$ is

$\frac{\sec 30°}{\mathrm{cosec} 60°}=$?

If $4 \tan \theta =3,$then $\left(\frac{4 \sin \theta - \cos \theta }{4 \sin \theta + \cos \theta }\right)$ is equal to

If $△ABC$ is a right-angled triangle at $C$ having $u$ units, $v$ units and $w$ units as the lengths of its sides opposite to the vertices $A, B, C$, respectively, then what is $\mathrm{tanA}+\mathrm{tanB}$ equal to ?

If $\sin \theta =\frac{1}{3}$, then the value of $2{\cot }^2\theta +2$ is equal to:

In fig. given, if $PS=14 \mathrm{cm}$, the value of $\tan a$ is equal to:

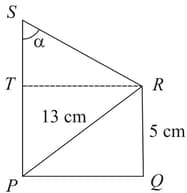
If $\sin \alpha =\frac{1}{2}$ and $\alpha$ is acute, then $(3\cos \alpha -4{\cos }^3\alpha )$ is equal to:

If $3\mathrm{cot\theta }=2$, show that $\frac{4\sin \theta -3\cos \theta }{2\sin \theta +6\cos \theta }=\frac{1}{3}$

If $\angle A$ and $\angle B$are acute angles such that $\tan A=\tan B$ then prove that $\angle A = \angle B$

If $5\tan \theta -4=0$, then the value of $\frac{5\sin \theta -4\cos \theta }{5\sin \theta +4\cos \theta }$ is