Volume of a Combination of Solids

 A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains $41\frac{19}{21} {\mathrm{m}}^3$ of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building in $\mathrm{m}$? 

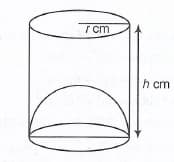
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is $\frac{\pi r^2}{3}\left[3h-2r\right].$

A solid ball is exactly fitted inside the cubical box of side $a.$ The volume of the ball is $\frac{4}{3}\mathrm{\pi }{a}^3.$

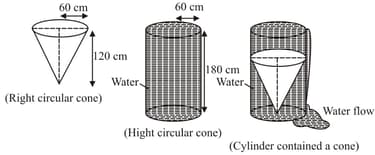
Water flows at the rate of $10 \mathrm{m} {\min }^{-1}$ through a cylindrical pipe $5 \mathrm{mm}$ in diameter. How long would it take to fill a conical vessel whose diameter at the base is $40 \mathrm{cm}$ and depth $24 \mathrm{cm}$?

A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimensions of cuboid are $10\mathrm{cm}, 5\mathrm{cm} \mathrm{and} 4\mathrm{cm}$. The radius of each of the conical depressions is $3\mathrm{cm}$. Find the volume of the wood in the entire stand.

The barrel of a fountain pen, cylindrical in shape, is $7 \mathrm{cm}$ long and $5 \mathrm{mm}$ in diameter. A full barrel of ink in the pin is used up on writing $3300$ words on an average. How many words can be written in a bottle of ink containing one-fifth of a litre?

How many cubic centimetres of iron is required to construct an open box whose external dimensions are $36 \mathrm{cm},25 \mathrm{cm}$ and $16.5 \mathrm{cm}$ provided the thickness of the iron is $1.5 \mathrm{cm}$. If one cubic centimetre of iron weighs $7.5 \mathrm{g}$, then find the weight of the box. 

A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and height of the cylinder are $6 \mathrm{cm}$ and $12 \mathrm{cm}$, respectively. If the slant height of the conical portion is $5 \mathrm{cm}$, then find the total surface area and volume of the rocket. $\left(\mathrm{use}:\pi =3.14\right)$.

A heap of rice is in the form of a cone of diameter $9\mathrm{m}$ and height $3.5 \mathrm{m}$. Find the volume of the rice. How much canvas cloth is required to just cover heap?

A solid right circular cone of height $120 \mathrm{cm}$ and radius $60 \mathrm{cm}$ is placed in a right circular cylinder full of water of height $180 \mathrm{cm}$ such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius to the cone.

$16$ glass spheres each of radius $2 \mathrm{cm}$ are packed into a cuboidal box of internal dimensions $16 \mathrm{cm}\times 8 \mathrm{cm}\times 8 \mathrm{cm}$ and then the box is filled with water. Find the volume of water filled in the box.

An ice-cream cone full of ice - cream having radius $5 \mathrm{cm}$ height $10 \mathrm{cm}$ as shown in figure

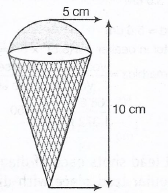
Calculate the volume of ice-cream, provided its $\frac{1}{6}$ part is left unfilled with ice-cream.

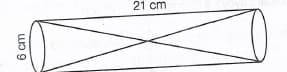
Two solid cones $A$ and $B$ are placed in a  cylindrical tube as shown in the figure. The ratio of their capacities is $2:1$. Find the heights and capacity of cones. Also, find the volume of the remaining portion of the cylinder.

From a solid cube of side $7 \mathrm{cm}$, a conical cavity of height $7 \mathrm{cm}$ and radius $3 \mathrm{cm}$ is hollowed out. Find the volume of the remaining solid.

Three metallic solid cubes whose edges are $3 \mathrm{cm}, 4 \mathrm{cm}$ and $5 \mathrm{cm}$ are melted and formed into a single cube. Find the edge of the cube so formed.

 If volumes of two spheres are in the ratio $64:27,$ then the ratio of their  surface areas is 

A medicine-capsule is in the shape of a cylinder of diameter $0.5 \mathrm{cm}$ with two hemispheres stuck to each of its ends. The length of entire capsule is $2 \mathrm{cm}$. The capacity of the capsule is

A metallic spherical shell of internal and external diameters $4 \mathrm{cm}$ and $8 \mathrm{cm},$ respectively is melted and recast into the form a cone of base diameter $8 \mathrm{cm}.$The height of the cone is

If a hollow cube of internal edge $22 \mathrm{cm}$ is filled with spherical marbles of diameter $0.5 \mathrm{cm}$ and it is assumed that $\frac{1}{8}$ space of the cube remains unfilled. Then, the number of marbles that the cube can accommodate is