ASA Congruence Rule

 In the adjoining figure, $\angle ABC=\angle ACB, D$ and $E$ are points on the sides $AC$ and $AB$ respectively such that $BE = CD$. Prove that, $OB=OC$.

 In the adjoining figure, $\angle ABC=\angle ACB, D$ and $E$ are points on the sides $AC$ and $AB$ respectively such that $BE=CD$. Prove that, $△OEB\cong △ODC$.

 In the adjoining figure, $\angle ABC=\angle ACB, D$ and $E$ are points on the sides $AC$ and $AB$ respectively such that $BE = CD$. Prove that  $△EBC\cong △DCB$

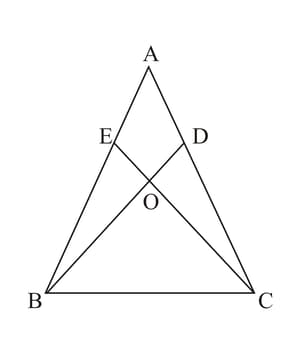
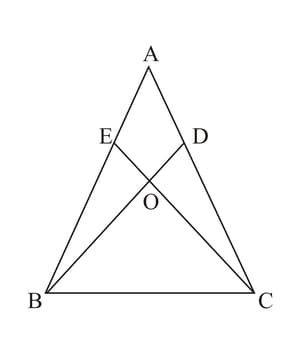
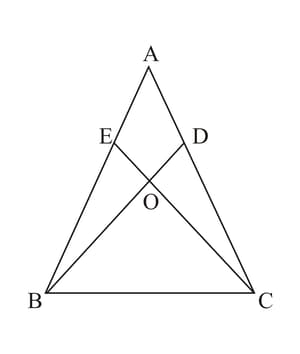
 In the adjoining figure, two lines $AB$ and $CD$ intersect each other at the point such that $BC\parallel DA$ and $BC= DA$. Show that $O$ is the mid-point of both the line segments $AB$ and $CD$.   

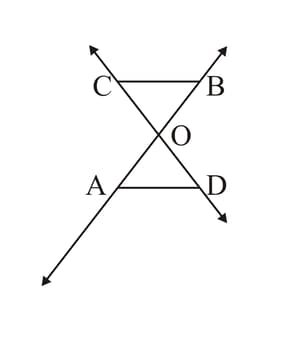
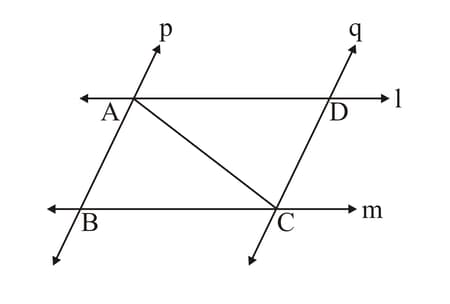
 In the adjoining figure, $l$ and $m$ are two parallel lines intersected by another pair of parallel lines $p$ and $q$. Show that $∆ABC \cong ∆CDA$.
   

 In the adjoining figure, $BM$ and $DN$ are perpendiculars to the line segment $AC$. If $BM = DN$, prove that $AC$ bisects $BD$.

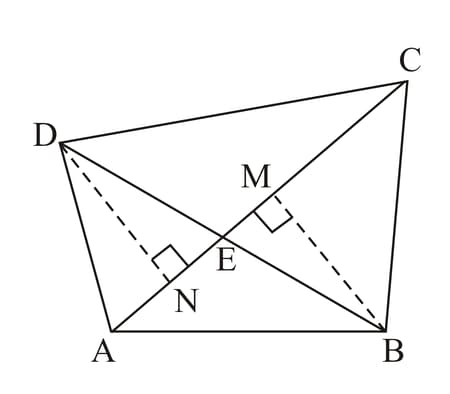
In the given figure, $AD$ is median of $△ABC, BM$ and $CN$ are perpendiculars drawn from $B$ and $C$ respectively on $AD$ and $AD$ produced. Prove that $BM=CN$.

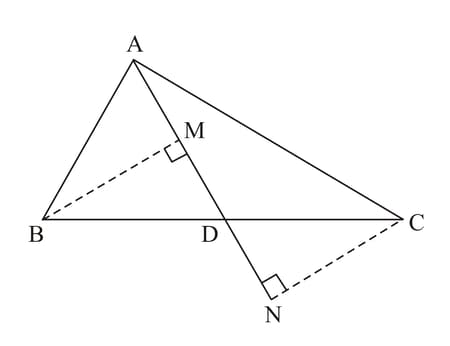
In triangles $ABC$ and $PQR, \angle A = \angle Q$ and $\angle B =\angle R$. Which side of $∆PQR$ should be equal to side $AB$ of $∆ABC$ so that the two triangles are congruent? Give reason for your answer.    

"If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent". Is the statement true? Why?

In triangles $ABC$ and $PQR, \angle A = \angle Q$ and $\angle B =\angle R$. Which side of $∆PQR$ should be equal to side $AB$ of $∆ABC$ so that the two triangles are congruent? Give reason for your answer.