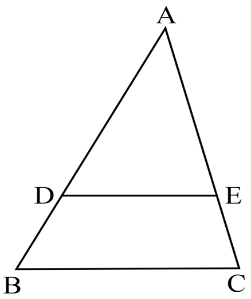
Basic Proportionality Theorem (Thales Theorem)
Important Questions on Basic Proportionality Theorem (Thales Theorem)
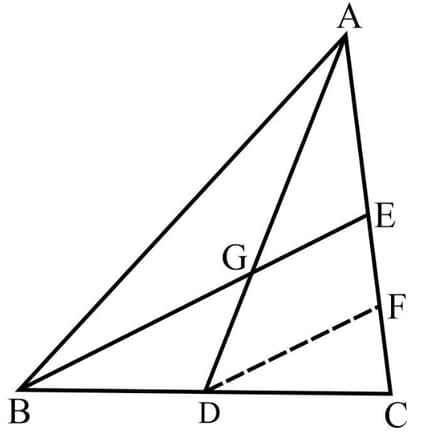
In the adjoining figure , medians and of meet at the point and is drawn parallel to Prove that and
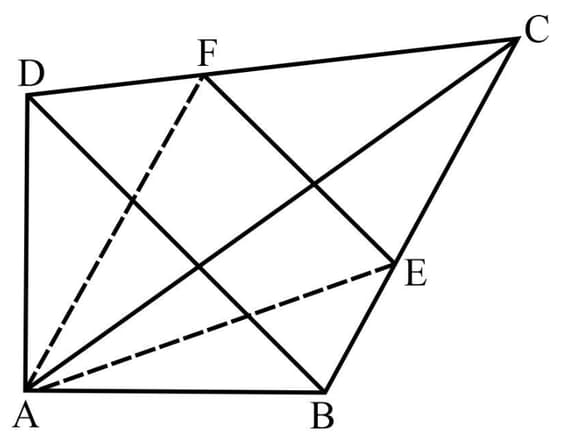
In the adjoining quadrilateral , The bisectors of and meet the sides and at the points and respectively. Prove that is parallel to
In a and are points on the sides and respectively such that, and Is ? Justify your answer.
In a and are points on the sides and respectively such that . If and find and
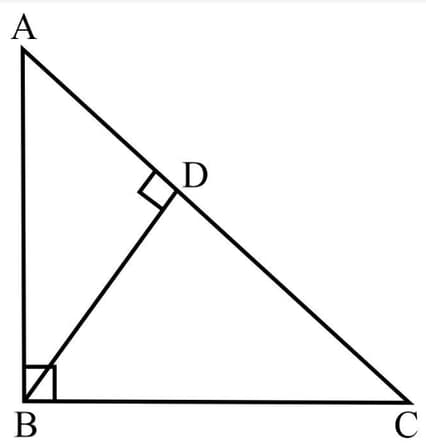
In the adjoining figure, is a triangle right-angled at and If and , find and
In the adjoining figure, line segment intersect the side of triangle at the point such that is mid-point of and . Prove that .
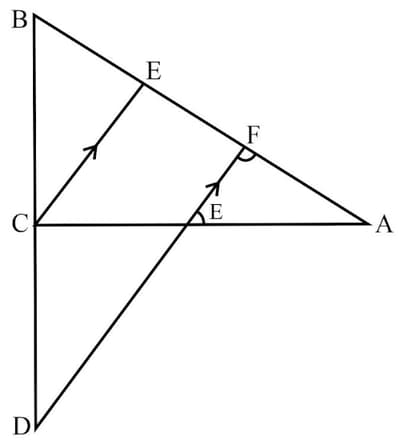
If the diagonals of a quadrilateral divide each other proportionally, prove that it is a trapezium.
d and E are respectively the points on the sides and of a such that and . Then the length of is
In the adjoining figure, . If and , then is
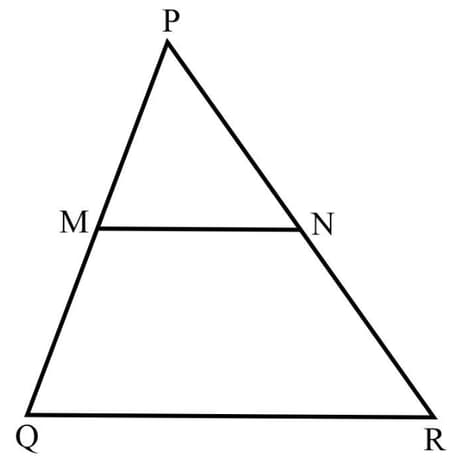
In the adjoining figure, and lengths are given in centimetres. The length of is
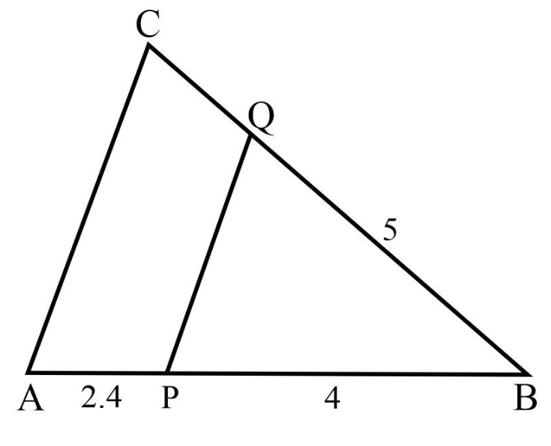
In the adjoining figure, and all measurements are in centimetres. The length of is
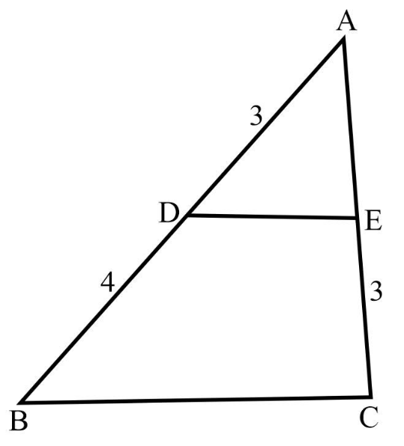
In the adjoining figure, and . Prove that is an isosceles triangle.
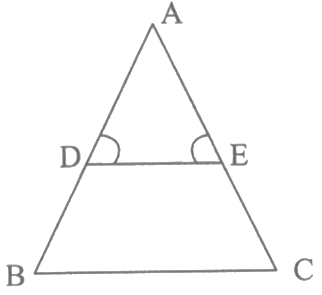
In the adjoining figure, . If and , find .
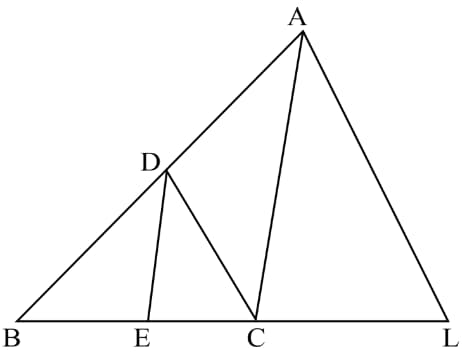
In figure given below, . Prove that .
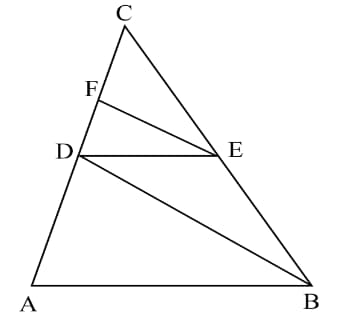
In figure given below, . Prove that is an isosceles triangle.
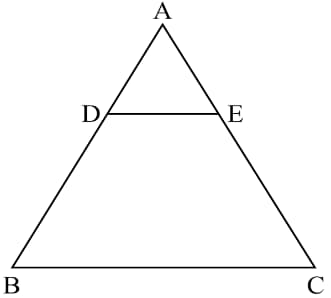
are points on the sides respectively of a triangle ABC such that and . Find whether or not.
and are respectively the points on the sides and of a triangle such that and . Is ? Give reasons for your answer.
and are points on the sides and respectively of a . For each of the following cases, state whether :
and
and are points on the sides and respectively of a . For the following case, state whether :
and
In the figure given below, are the points on sides respectively. such that . If .Find the value of .