Trigonometric Ratios of Some Specific Angles
Trigonometric Ratios of Some Specific Angles: Overview
This topic covers concepts, such as, Trigonometric Ratios of 90 Degree, Trigonometric Ratios of 45 Degree,Trigonometric Ratios of 0 Degree and Trigonometric Ratios of 30 Degree etc.
Important Questions on Trigonometric Ratios of Some Specific Angles
If and , then the value of is:
If , then value of is:
If , then what is the value of when ?
Find the value :
If then the value of
If , then what is the value of ?
If , show that
In an acute angled triangle , if and , then find and .
If and , then find the value of .
If , then find the value of
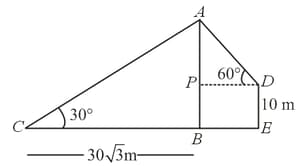
A tower and a building are standing vertically on a level ground. The angles of elevation of the top of the tower from a point on the same ground and from the top of the building are found to be respectively. If the distance of the point from the foot of the tower is and height of the building is , then find the distance between the foot of the tower and building and also the distance between their tops.
In a rectangle , the length is twice the width . Pick a point on side such that the lengths of and are equal. The measure of angle is:
What is the value of ?
Find the value of
Given that
Find when
for all values of .
The angle of elevation of the top of a rock from the top and foot of a high tower are respectively. Find the height of the rock.
If , then find .
Prove that .
