Trigonometric Ratios

$\sin \left(90°\right)$ is

Explain why ${\sin }^{-1}\theta \ne \frac{1}{\sin \theta }$, but ${\sin }^2\theta ={\left(\sin \theta \right)}^2$.

For the triangle $ABC$ shown below, $\sin B=k$. The size of the triangle $ABC$ is increased in such a way that area of the new triangle is double, keeping the angles equal. This produced $∆PQR$. Then, the value of $\sin Q$ will be

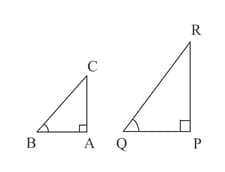
Trigonometric ratios are dependent on the size of the triangle provided the angle remains the same.

Prove that Trigonometric ratios are independent of the size of the triangle provided the angle remains the same.

$\cot \mathrm{A}=\cos \mathrm{A}\times \sin \mathrm{A}$.

If $\cot A+\frac{1}{\cot A}=1$, then the value of ${\cot }^{2}A+\frac{1}{{\cot }^{2}A}$ is

if $4 \sin \theta -3 \cos \theta =0$ find the value of $4 {\cos }^2\theta -3 {\sin }^2\theta +2$

Use Fig. to find the value of 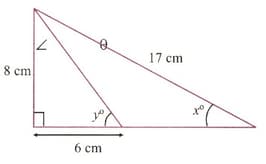$3 \tan x^0-2 \sin y^0 + 4 \cos y^0$ 

In Fig ABC is a right triangle, righrt angled at B. Given that $\angle \mathrm{ACB}=\mathrm{\theta }$ side $\mathrm{AB}=2 \mathrm{cm}$ and side $\mathrm{BC}=1 \mathrm{cm}$, find the value of  ${\sin }^2\theta +{\cos }^2\theta$.

If $2 \sin x = \sqrt{3}$, then evaluate $4 {\sin }^{3}x - 3 \sin x$

Find the value of $\tan \left(\alpha \right)$ from the given triangle $∆ABC$

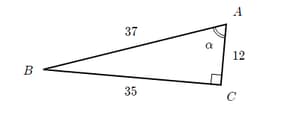
In a $△\mathrm{ABC},$$\mathrm{AD}\perp \mathrm{BC}$ if $\tan \mathrm{B} =\frac{3}{4}$ and $\tan \mathrm{C} = \frac{5}{12}$ and $\mathrm{BC} = 56 \mathrm{cm}$ calculate the lengths of $\mathrm{AD}$  

Find the trigonometric ratios in standard position whose terminal arm passes through the points $\left(-6, 8\right)$

If $\cos \theta =\frac{-7}{25}$ and $\theta$ is in second quadrant, find the remaining trigonometric ratios.

Find the sine ratio in standard position where terminal arm passes through $\left(-5,-12\right)$.

if $3 \sin \theta = 4 \cos \theta$, find the value of $4 {\sin }^2\theta - 3 {\cos }^2\theta + 2$

if $\tan \theta =\frac{20}{21}$, find the value of $\frac{1+\sin \theta + \cos \theta }{1 - \sin \theta + \cos \theta }$

if $\sin \theta =m$, find the value of ${\tan }^2\mathrm{\theta }-\frac{1}{{\cos }^2\mathrm{\theta }}$

A tower stands vertically on the ground. At a point on the ground, which is $15$ m away from the foot of the tower, the tower subtends an angle of ${60}^0$. Find the height of the tower.