Inradius, Exradii and Circumradius

If in a triangle product of sides is $12$ and area of the triangle is $3$, then find the circumradius.

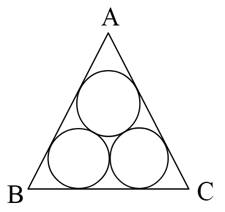
In a triangle $ABC$, $3$ coins of radii $1$ cm each are kept so that they touch each other and also the sides of triangle as shown. The side (in units) of the triangle is

In a $△ABC$, If $\frac{r_1}{bc}+\frac{r_2}{ca}+\frac{r_3}{ab}=\frac{1}{r}-\frac{1}{nR}$ then the value of $n$ is

Mention the formulae to find the in-radius (Apothem) of a regular polygon, when its (a) side length is given (b) circum-radius is given

Prove that in any $\Delta ABC, R+r\ge \min \left({\ell }_a,{\ell }_b,{\ell }_c\right)$, where $R$ is the circumradius, $r$ the inradius, and ${\ell }_a,{\ell }_b,{\ell }_c$ the angle bisectors of the triangle.

If $R\left(a+b\right)=c\sqrt{ab}$, where $a,b,c$ are sides of $∆ABC$ and $R$ is circumradius, then $\cos \left(\frac{C}{2}\right)\sin \left(\frac{C}{3}\right)=\_\_\_\_\_$

If $\left(1-\frac{r_1}{r_2}\right)\left(1-\frac{r_1}{r_3}\right)=2$, then prove that the triangle is right-angled.

In any $∆ABC$, prove that

(i) $\left(r_3+r_1\right)\left(r_3+r_2\right)\sin C=2r_3\sqrt{r_2{r}_3+r_3{r}_1+r_1{r}_2}$.

In an acute-angled triangle $ABC, r+r_1=r_2+r_3$ and $\angle B>\frac{\mathrm{\pi }}{3}$, then prove that $b+3c<3a<3b+3c$.

For next two question please follow the same 

Tangents that are drawn from the point $P(3,4)$ to the circle $S\equiv x^2+y^2-9=0$ that meets the circle at $A \& B$ . If for circle $S_1=0, S=0$ is the director circle and for the circle $S_2=0$ , its succeeding circle. Suppose, if the $\Delta PAB$ is called as tangent triangle of the circle $S=0$ . Let$A_1,B_1 ; A_2,B_{2 }; A_3,B_3,..$ be the points of contacts of tangents drawn from $P$ to the circles$S_1=0, S_2=0, ... \& P{A}_1{B}_1, P{A}_2{B}_2, P{A}_3{B}_3,...$ be the corresponding tangent triangles. Here, director circle is the locus of point of intersection of perpendicular tangents with respect to a (circle).

 The inradius ( in units ) of the $\Delta PAB$ is

If $\mathrm{l}$ has greatest possible integer value then $∆\mathrm{ABC}$ is

Greatest integer value of $l$ is

. Least integer value of $\mathrm{l}$ is

$\frac{{\mathrm{r}}_1^{\text{'}}}{\mathrm{R}}=$

$\frac{{\mathrm{r}}^{\text{'}}}{\mathrm{R}}=$

$\frac{s^{\text{'}}}{R}=$

The inradius $\mathrm{r}$ is given by

$\mathrm{EF}=$

If $\frac{\mathrm{bx}}{\mathrm{c}}+\frac{\mathrm{cy}}{\mathrm{a}}+\frac{\mathrm{az}}{\mathrm{b}}=\frac{{\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2}{\mathrm{k}}$, then the value of $\mathrm{k}$ is 

Using the range of $\mathrm{B}$, we finally get the minimum perimeter $=$