Heights and Distances

A tower and building are standing vertically on a level ground. The angles of elevation of the top of the tower from a point on the same ground and from the top of the building are found to be $30°$ and $60°$ respectively. If the distance of the point from the foot of the tower is $30\sqrt{3} \mathrm{m}$ and height of the building is $10 \mathrm{m}$, then find the distance between the foot of the tower and building and also the distance between their tops.

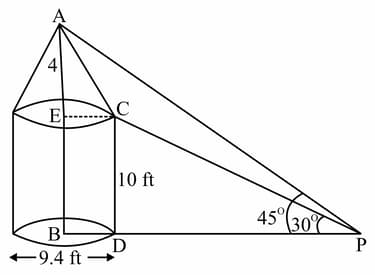
A building on the ground is in the form of a conical tomb surmounted by a cylinder of height $10$ feet as shown in figure. From a point 'P' on the same ground, the angle of elevation of the top edge of the cylinder is found to be $30°$ and the angle of elevation to the vertex of the cone is found to be $45°$. If the diameter of the outer edge of circular base of the cylinder is $9.4$ feet, find the height of the conical shaped tomb.

(Take $\sqrt{3}=1.73$)

Which of the following cannot be done with the help of theodolite in surveying?

The angle of elevation and depression are usually measured by a device called

A person is standing at a distance of $80 \mathrm{metres}$ from a Church and looking at its top. The angle of elevation is of $45°$. Find the height (in $\mathrm{m}$) of the Church.

If $AB=4 \mathrm{m}$ and $AC=8 \mathrm{m}$, then angle of elevation of $A$ as observed from $C$ is (write answer without degree symbol)

If the length of the shadow of a tower is increasing, then the angle of elevation of the sun

The angle of elevation of an aircraft from a point on horizontal ground is found to be $30°$. The angle of elevation of same aircraft after $24$ seconds which is moving horizontally to the ground is found to be $60°$. If the height of the aircraft from the ground is $3600\sqrt{3} \mathrm{m}$, find the velocity of the aircraft (in $\mathrm{m}/\mathrm{s}$).

The angles of elevation of the top of a tower from two points at a distance of $4 \mathrm{m}$ and $9 \mathrm{m}$ from the base of the tower and in the same straight line with it are complementary. Find the height of the tower in metre.

A tree is broken by the wind. The top of that tree struck the ground at an angle of $30°$ and at a distance of $30 \mathrm{m}$ from the root. Find the height (in $\mathrm{m}$) of the whole tree.$\left(\sqrt{3}=1.73\right)$

The angles of elevation of the top of a tower from two points at a distance of $9 \mathrm{m}$ and $25 \mathrm{m}$ from the base of the tower in the same straight line are complementary. Find the height of the tower in $\mathrm{m}$.

If the ratio of the length of a vertical bar to its shadow is $1:\sqrt{3}$, then find the elevation angle of the sun in degrees.

A tower and a pole stand vertically on the same level ground. It is observed that the angles of depression of top and foot of the pole from the top of the tower of height $60 \mathrm{m}$ is $30°$ and $60°$ respectively. Find the height of the pole in metre.

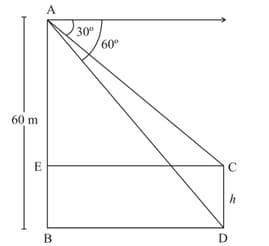
From a point on the ground which is $120\mathrm{m}$ away from the foot of the unfinished tower, the angle of elevation of the top of the tower is found to be ${30}^{\circ }$. Find how much height of tower has to increased in metre (up to one decimal place) so that its angle of elevation at the same point become ${60}^{\circ }$? (Take $\sqrt{3}=1.73$)

A kite is flying at a height of $75$ metres from the level of ground attached to a string inclined at $60°$ to the horizontal. Find the length of the string in meters correct up to one decimal place. [Use $\sqrt{3}=1.73$]

A person is standing at a distance of $80 \mathrm{metres}$ from a Church and looking at its top. The angle of elevation is of $45°$. Find the height (in $\mathrm{m}$) of the Church.

A theodolite is a precision optical instrument for measuring used to measure the speed of sound in a liquid.

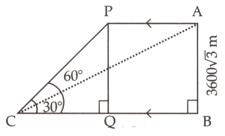
Two climbers are at points $\mathrm{A} \mathrm{and} \mathrm{B}$ on a vertical cliff face. To an observer $\mathrm{C}$, $40\mathrm{m}$ from the foot of the cliff, on the level ground, $\mathrm{A}$ is at an elevation of  $48°$ and $\mathrm{B} \mathrm{of} 57°$. FInd $k,$ if the distance between the climbers is $k \mathrm{m}.$ Take  $\tan {57}^{\circ }=1.537; \tan {48}^{\circ }=1.110$.

The angle of elevation of a cloud from a point $20 \mathrm{m}$ above a lake (point $\mathrm{A}$) is $30°$. The angle of depression of its reflection form point $\mathrm{A}$ is $60°$. If the distance of the cloud form point $\mathrm{A}$ is $x \mathrm{m}$, then find the value of $x$.

If angle of elevation of sun changes from $30°$ to $60°$. Then at these angles of elevation find the difference in the length of shadow of $15 \mathrm{m}$ high pillar.