Kirchhoff's Laws With Capacitors

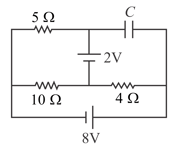
Calculate the potential difference across the capacitor in the circuit (in Volts). (Approximate the answer to the nearest integer)

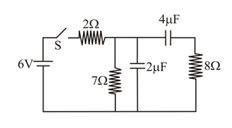
In the circuit shown in figure the switch $S$ is initially open and both the capacitors are initially uncharged. If the ratio of current through $2\Omega$ resistor, just after the switch $\mathrm{S}$ is closed and a long time after the switch $\mathrm{S}$ is closed is $\frac{x}{2}$, find the value of $x$.

Three capacitors are connected as shown in the figure. Then the charge on capacitor plate $C_1$ is,

Two capacitors of $2 \mathrm{\mu }\text{F}$ and $3 \mathrm{\mu }\text{F}$ are connected in series. The potential at point $A$ is $1000 \mathrm{V}$ and the outer plate of $3 \mathrm{\mu }\text{F}$ capacitor is earthed. The potential at point $B$ is, 

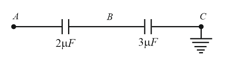
Three uncharged capacitors of capacities $C_1,C_2$ and $C_3$ are connected as shown in the figure. $A,B$ and $C$ are at potentials $V_1, V_2$ and $V_3$ respectively. The potential at $O$ is

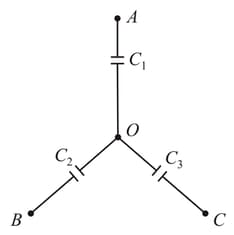
The equivalent capacitance between the points $A$ and $B$ is

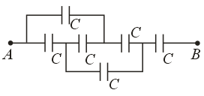
A capacitor $C_1=1\mu f$ and $C_2=2\mu f$ are charged with switch in position $\left(1\right).$ Now switch is shifted to position $\left(2\right).$ Capacitor $C_3=3\mu f$ is initially uncharged. The ratio of potential difference on $C_1$ and $C_3$ is:

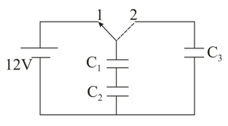
In the given figure, three capacitors $C_1, C_2$ and $C_3$ are joined to a battery, with symbols having their usual meanings, the correct conditions will be:-

In the figure a potential of $+1200 \mathrm{V}$ is given to point $A$ and point $B$ is earthed, what is the potential at the point $P:$

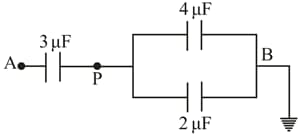
A charge of $8 \mathrm{\mu C}$ is given to point $A$ and point $B$ is earthed. If each capacitance is $1 \mathrm{\mu F}$, what is the total energy (in $\mathrm{\mu J}$ ) of the system ?

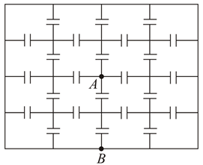
Three uncharged capacitors of capacitance $C_1,C_2$ and ${\mathrm{C}}_3$ are connected as shown in the figure to one another at point $O$. Points $A, B$ and $D$ are at potentials $V_A,$ $V_B$ and $V_D$ respectively. Then the potential at $O$ will be,: 

The charge on the capacitor $\mathrm{C}$ in steady state is ${\mathrm{q}}_1$ in the given diagram. Now, key is closed and steady state charge on $\mathrm{C}$ is ${\mathrm{q}}_2$ .The ratio of charges ${\mathrm{q}}_1 \mathrm{and} {\mathrm{q}}_2$ will be -

A capacitors of plate area $\mathrm{A}$ and mass ${\mathrm{m}}_2$ of each plate is charged upto charge $\mathrm{q}$ . The lower plate is rigidly fixed as shown in figure. Find the value of ${\mathrm{m}}_1$ so that the system remain in equilibrium -

In the given circuit switch $\mathrm{K}$ is open. The charge on the capacitor is $\mathrm{\prime }\mathrm{C}\mathrm{\prime }$ in this steady state is ${\mathrm{q}}_1$ . Now key is closed and steady state charge on $\mathrm{C}$ is ${\mathrm{q}}_2$ . The ratio ${\mathrm{q}}_1/{\mathrm{q}}_2$ is -

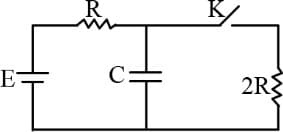
In steady state, charge on $\mathrm{3 }\mathrm{\mu }\mathrm{F}$ capacitor is

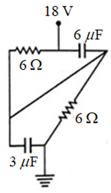
In the adjacent circuit $V_A–V_B$ will be:
  

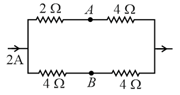
In the circuit of following figure, the final voltage drop across the capacitor $\mathrm{C}$ in steady state is

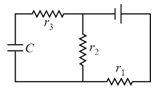
Two condensers $C_1$ and $C_2$ in a circuit are joined as shown in figure. The potential of point $A$ is $V_1$ and that of $\mathrm{B}$ is $V_2$ . The potential of point $D$ will be

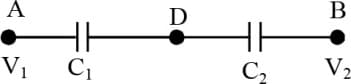
In the circuit shown in the figure, a potential difference of $60\mathrm{ }\mathrm{V}$ is applied between $\mathrm{a}$ and $\mathrm{b}$. The potential difference between the points $\mathrm{c}$ and $\mathrm{d}$ is

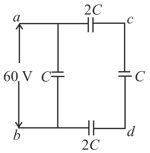
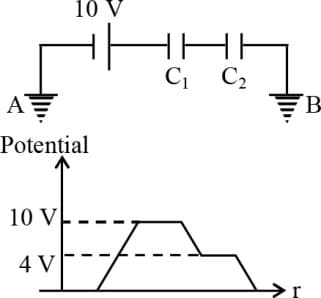
The figure shows two capacitors $C_1$ and $C_2$ connected with $10\mathrm{ }\mathrm{V}$ battery and terminals $A$ and $B$ are earthed. The graph shows the variation of potential as one moves from left to right. Then the ratio of $\frac{{\mathit{C}}_{\mathit{1}}}{{\mathit{C}}_{\mathit{2}}}$ is