Kirchhoff's Laws and Their Applications
Kirchhoff's Laws and Their Applications: Overview
This topic covers concepts, such as, Kirchhoff's Law, Kirchhoff's First Law, Kirchhoff's Second Law, Method to Solve Complex Circuit Using Kirchhoff's Law & Finding Potential Difference between Two Points in an Electrical Circuit etc.
Important Questions on Kirchhoff's Laws and Their Applications
Which of the following rule may be used to obtain the values of the three unknown currents in the branches (shown) of the circuit given below?
Apply Kirchhoff’s rule to the loops and to find currents and in the network.
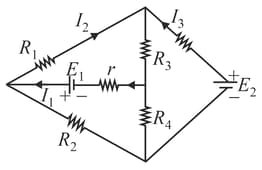
Apply Kirchhoff’s rules to the loops and to write the expressions for the currents and in the network.
State Kirchhoff’s rules. Use these rules to write the expressions for the currents and in the circuit diagram shown.

Two cells of emf and and internal resistance and respectively are connected in parallel to pass a current in the same direction through an external resistance of .
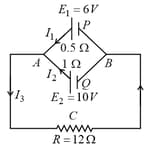
Using Kirchhoff’s laws, calculate the current through each branch of the circuit and potential difference across the resistor.
Explain Kirchhoff's laws with examples.
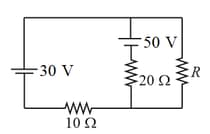
A battery of internal resistance is connected to the network of resistances, as shown in the figure. In order that the maximum power can be delivered to the network, the value of in should be
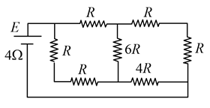
As the switch is closed in the circuit, the current passed through it is (in )
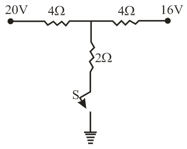
Four resistances and make the arms of a quadrilateral Across is a battery of emf and internal resistance negligible. The potential difference across in is __________ .
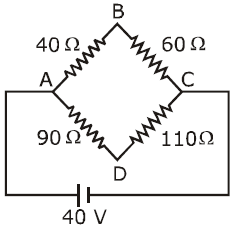
In the circuit shown in the figure, reading of voltmeter is when is closed, reading of voltmeter is when only is closed and reading of voltmeter is when both and are closed. Then -
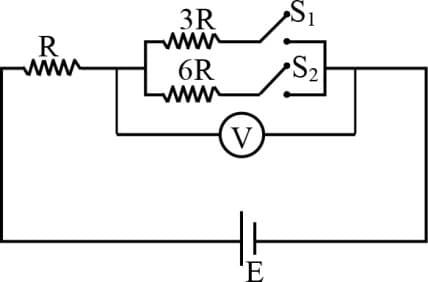
The series combination of two batteries, both of the same emf but different internal resistance of and is connected to the parallel combination of two resistors and The voltage difference across the battery of internal resistance is zero, the value of in is......
In the circuit shown, the value of in ohm that will result in no current through the battery, is:
Kirchhoff's first law and second law, proves the
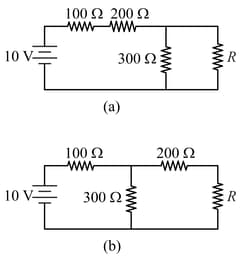
A student was trying to construct the circuit shown in the figure below marked (a), but ended up constructing the circuit marked (b). Realizing her mistake, she corrected the circuit, but to her surprise, the output voltage (across ) did not change.
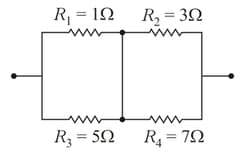
The value of resistance is :-
Kirchhoff's first law is based on conservation of
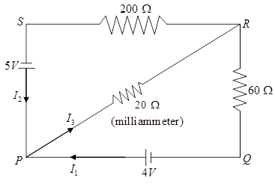
Find the magnitude of flowing current in of following circuit, when a constant voltage is kept between
A cell with internal resistance and cell with internal resistance and external resistance are connected in parallel. The current in ampere through cell is
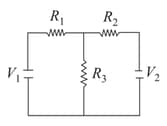
Consider the circuit as shown below. In the circuit and The current flowing through resistance is
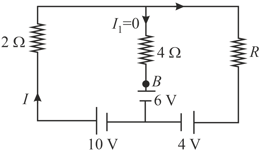
Find the current I in the circuit below that flows through resistor.
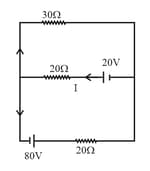
For what value of in the circuit as shown, the current through will be zero ?