Kirchhoff’s Laws of Electrical Network

Which of the following rule may be used to obtain the values of the three unknown currents in the branches (shown) of the circuit given below?

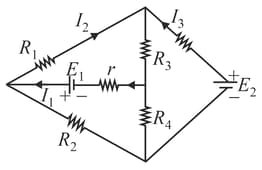
Apply Kirchhoff’s rules to the loops $ACBPA$ and $ACBQA$ to write the expressions for the currents  $I_1, I_2$  and  $I_3$  in the network.

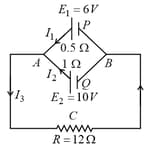
State Kirchhoff’s rules. Use these rules to write the expressions for the currents  $I_1, I_2$ and $I_3$ in the circuit diagram shown.

Explain Kirchhoff's laws with examples.

A battery of internal resistance $4 \mathrm{\Omega }$ is connected to the network of resistances, as shown in the figure. In order that the maximum power can be delivered to the network, the value of $\mathrm{R}$ in $\mathrm{\Omega }$ should be

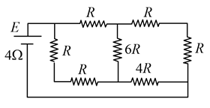
In the circuit shown in the figure. $\left(\mathrm{A}\right)$, $R_3$ is a variable resistance



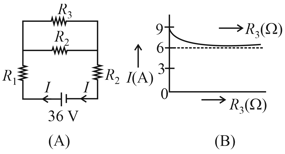
As the value $R_3$ is changed, current $I$ though the cell varies as shown. Obviously, the variation is asymptotic, i.e. $I\mathrm{ }\to \mathrm{ }6 \mathrm{A}$ as $R_3\to \mathrm{\infty }$ . Ratio of resistances $R_1 \text{and} R_2$ will be: 

What is Kirchhoff's current law formula?

What does Kirchhoff's current law say?

What is the sign convention in battery technology?

What do you mean by sign convention?

What is Kirchhoff's 2nd law write down the sign convention for currents and EMF s?

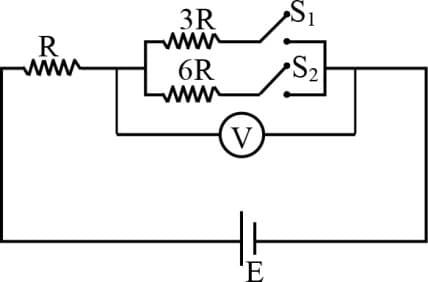
In the circuit shown in the figure, reading of voltmeter is $V_1$ when $S_1$ is closed, reading of voltmeter is $V_2$ when only $S_2$ is closed and reading of voltmeter is $V_3$ when both $S_1$ and $S_2$ are closed. Then -

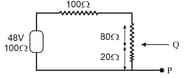
In the circuit shown, the potential difference across $PQ$ will be nearest to 

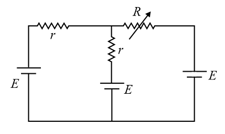
In the shown circuit the resistance $R$ can be varied

The variation of current through $R$ against $R$ is correctly plotted as:

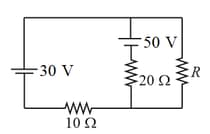
In the circuit shown, the value of $R$ in ohm that will result in no current through the $30 \mathrm{V}$ battery, is:

Kirchhoff's first law and second law, proves the

Consider the part of the circuit shown. What is the value of current $I,$ if the battery is ideal?

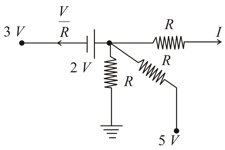
Kirchhoff's first law is based on conservation of

Kirchhoff’s second law states that the total sum of currents entering into a node is zero.