Application of Ampere's Law

A cylindrical conductor of radius $R$ carries a current along its length. The current density $J$, however, is not uniform over the cross-section of the conductor but is a function of the radius according to $J=br$, where $b$ is a constant. Then the expression for the magnetic field



$\left(B_1\right)$ at $r_1<R$ and
$\left(B_{\mathrm{2}}\right)$ at distance $r_2>R$, measured from the axis is:

Using Ampere’s circuital law,obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.

When the number of turns in a toroidal coil is doubled, then the value of magnetic flux density will become,

Find the magnetic field created by a current carrying wire of current $2 \mathrm{A}$ at a distance of $10 \mathrm{cm}$ from the wire in micro Telsa.

The two ends of $\mathrm{a}$ non-conducting spring of force constant $50{\mathrm{Nm}}^{-1}$ and unstretched length of $2 \mathrm{cm}$ are connected to the mid points of two straight parallel rods each of length $4 \mathrm{m}$. When $100 \mathrm{A}$ current is passed through each rod in the same direction, the work done on the spring in $\mathrm{mJ}$ is

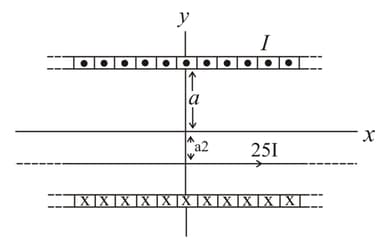
An infinitely long solenoid of radius a $=\frac{5}{\pi }\mathrm{cm}$ and $10 \mathrm{turns} {\mathrm{cm}}^{-1}$ is placed such that its axis of symmetry lies along the $X$-axis. A current $I$ is flowing through the solenoid ( $X$ means that $I$ is flowing into and $·$ means it is flowing out of the page). A straight infinite wire with current $25 I$ is placed parallel to the $X-$axis at a distance $\frac{a}{2}$ away from the center. Which of the following gives the direction of net magnetic field at the origin?

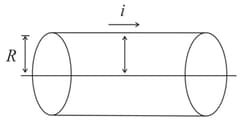
 Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.

Two long parallel wires having current $I$ and $3I$ in the same direction are $4 \mathrm{m}$ apart. Find the point where magnetic due to both is zero.

A wire on horizontal plane has a current of $50 \mathrm{A}$ in south to North direction. Find the magnitude and direction of magnetic field at point $2.5 \mathrm{m}$ towards east.

A long straight wire has a current $35 \mathrm{A}$. Find magnetic field at a distance of $10 \mathrm{cm}.$

A solenoid has length $0.5 \mathrm{m}$. Its winding is in double layer, each layer having $500$ turns. Its radius is $1.4 \mathrm{cm}$. Find magnetic field at its center when current in it is $5 \mathrm{A}$.

A $1.0 \mathrm{m}$ long solenoid has $100$ turns. Its radius is $1 \mathrm{cm}$. Find magnetic field at its axis, if current in it is $5 \mathrm{A}$. Find the force on electron moving with velocity ${10}^4 \raisebox{1ex}{$\mathrm{m}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{s}$}\right.$ along the axis.

Compare magnetic field of a bar magnet and a current-carrying solenoid. 

Write down the value of magnetic field inside a copper pipe of radius $R$ and current $I$.

A long solenoid has six layers of windings of $450$ turns each. If diameter is $2.2 \mathrm{cm}$, length is $90 \mathrm{cm}$ and current carried is $6 \mathrm{A}$, then calculate the magnitude of magnetic field inside the solenoid.

The current density $\mathrm{J}$ inside a long, solid, cylindrical wire of radius $\mathrm{a}=12\mathrm{ }\mathrm{m}\mathrm{m}$ is in the direction of the central axis, and its magnitude varies linearly with radial distance $\mathrm{r}$ from the axis according to $\mathrm{J}=\frac{{\mathrm{J}}_0\mathrm{r}}{\mathrm{a}},$ where ${\mathrm{J}}_0=\frac{{10}^5}{4\mathrm{\pi }}\frac{\mathrm{A}}{{\mathrm{m}}^2}.$ Find the magnitude of the magnetic field at $\mathrm{r}=\frac{\mathrm{a}}{2}$ in $\mathrm{\mu }\mathrm{T}.$

A long solenoid is fabricated to closely winding wire of radius $0.5 \mathrm{m}\mathrm{m}$ over a cylindrical frame, so that the successive turns nearly touch each other. The magnetic field at the centre of solenoid, if it carries a current of $5 \mathrm{A}$ is.

The turns of a solenoid, designed to provide a given magnetic flux density along its axis, are wound to fill the space between two concentric cylinders of fixed radii. How should the diameter $d$ of the wire used be chosen so as to minimize the heat dissipated in the windings?

An iron ring of relative permeability has windings of insulated copper wire of n turns per metre. When the current in the windings is I, find the expression for the magnetic field in the ring. (b)Identify the type of magnetic material. Draw the modification of the field pattern on keeping a piece of this material in a uniform magnetic field.

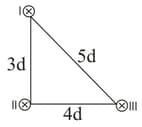
Three long wires, each carrying current $i$ are placed parallel to each other. The distance between I and II is 3d, between II and III is 4d and between III and I is 5d. Magnetic field at the position of wire II is