Gauss’s Law and Its Applications
Gauss’s Law and Its Applications: Overview
This topic covers concepts, such as, Gauss Theorem in Electrostatics, Condition for the Validity of Gauss Theorem, Electric Field due to a Long Charged Cylinder Using Gauss's Law & Electric Field inside a Thick Charged Plate Using Gauss's Law etc.
Important Questions on Gauss’s Law and Its Applications
Which law is used to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities and respectively:
Applying Gauss theorem, the expression for the electric field intensity at a point due to an infinitely long, thin, uniformly charged straight wire is
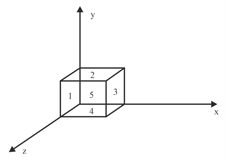
In a region of space, the electric filed , Consider imaginary cubical volume of edge with its edges parallel to the axes of coordinates. Now
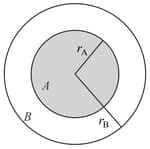
In the figure, the inner (shaded) region represents a sphere of radius , within which the electrostatic charge density varies with the radial distance from the center as , where is positive. In the spherical shell of outer radius , the electrostatic charge density varies as . Assume that dimensions are taken care of. All physical quantities are in their SI units.
Which of the following statement(s) is/(are) correct?
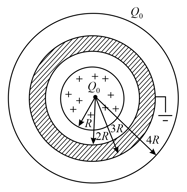
An insulated sphere with dielectric constant (where ) of radius of is having a total charge uniformly distributed in the volume. It is kept inside a metallic sphere of inner radius and outer radius . Whole system is kept inside a metallic shell of radius , metallic sphere is earthed as shown in the figure. Spherical shell of radius is given a charge . Consider graph for only. Where and represents electric field and radial distance from the centre respectively. Then choose the CORRECT option(s)
Three uniformly charged infinite wires with linear charge density are placed along and axis respectively. Find the flux of electric field through Gaussian surface given by If your answer is fill the value of
The electric field due to unknown charge distribution is given by , where is a constant in SI units. The total charge (in coulombs) in overall space is equal to
A spherical non-conducting shell of uniform charge density has a small circular hole cut out of it as shown in the figure. What is magnitude of the electric field just inside the sphere, directly below the centre of the circular hole?
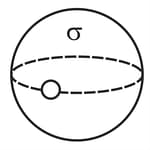
A conducting sphere of radius and charge is surrounded by a medium of resistivity at Due to the medium the charge starts decreasing from it. At the charge on the sphere is found then the value of is [Absolute permittivity of the vacuum is ]
A non-conducting cylinder of radius is infinitely long. Its volume charge density varies linearly as the distance from the axis of the cylinder. If is zero at the axis and is on the surface, the electric intensity due to it is :
A charge is located at . The flux through the shaded region is .
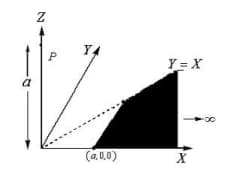
Find .(The region which is shaded is enclosed by lines and and extends upto )
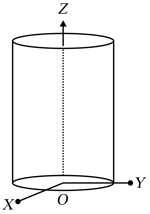
The electric field in the space is given by Consider a right circular cylindrical surface whose radius is '' and height ' '. Now choose the correct option(s).
A hollow charged metal sphere has radius . If the potential difference between its surface and a point at a distance from the centre is, then electric field intensity at a distance is:
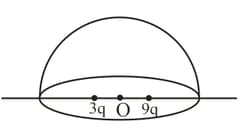
In the shown figure a hemisphere is placed and two charges and are placed symmetrically about centre Net electric flux over curved surface is given as where and are lowest possible integers then value of is :
The electric field in a region is radially outwards with magnitude In a sphere of radius centered at the origin, calculate the value of charge in coulombs if and
A sphere of radius have volume charge density given as
for
for
If electric field at distance from centre is Then will be.
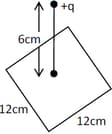
A point charge of is at a distance vertically above the centre of a square of side as shown in figure. The magnitude of the electric flux through the square will be _________ (Write the value to the nearest integer)
A circular disc of radius carries surface charge density where is a constant and r is the distance from the center of the disc. Electric flux through a large spherical surface that encloses the charged disc completely is Electric flux through another spherical surface of radius and concentric with the disc is The ratio , find the value of .
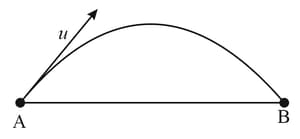
In the figure shown, there is a large sheet of charge of uniform surface charge density . A charge particle of charge and mass is projected from a point on the sheet with a speed with angle of projection such that it lands at maximum distance from on the sheet. Neglecting gravity, find the time of flight.
The total flux through the faces of the cube with side of length if a charge is placed at corner of the cube is