Ampere’s Circuital Law

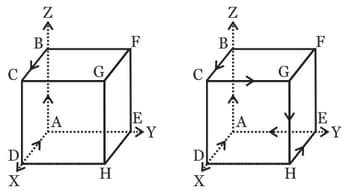
Current I is following along the path ABCD, along the four edges of the cube (figure-a) creates a magnetic field in the centre of the cube of ${\text{B}}_0$. Find the magnetic field B created at the centre of the cube current I following along the path of the six edges ABCDHEA figure - b

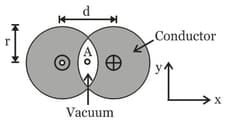
Two long conductors are arranged as shown above to form overlapping cylinders, each of radius r, whose centres are separated by a distance d. Current of density J flows into the plane of the page along the shaded part of one conductor and an equal current flows out of the plane of the page along the shaded portion of the other, as shown. What are the magnitude and direction of the magnetic field at point A ?

A cylindrical conductor of radius $R$ carries a current along its length. The current density $J$, however, is not uniform over the cross-section of the conductor but is a function of the radius according to $J=br$, where $b$ is a constant. Then the expression for the magnetic field



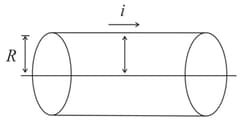
$\left(B_1\right)$ at $r_1<R$ and
$\left(B_{\mathrm{2}}\right)$ at distance $r_2>R$, measured from the axis is:

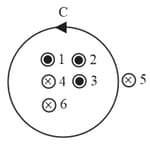
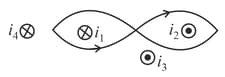
Six wires of current ${\mathrm{I}}_1=\mathrm{1 }\mathrm{A},{\mathrm{I}}_2=\mathrm{2 }\mathrm{A},{\mathrm{I}}_3=\mathrm{3 }\mathrm{A},{\mathrm{I}}_4=\mathrm{1 }\mathrm{A},{\mathrm{I}}_5=\mathrm{5 }\mathrm{A}$ and ${\mathrm{I}}_6=\mathrm{4 }\mathrm{A}$ cut the page perpendicularly at the points $\mathrm{1,\; 2,\; 3,\; 4,\; 5}$ and $6$ respectively as shown in the figure. Find the value of integral $\oint \overrightarrow{B}.d\overrightarrow{l}$ around the circular path $\mathrm{C.}$

A circuit is in the form of a regular hexagon of side $a$ with its centre at the point $O$. A current $I$ flows in the circuit.

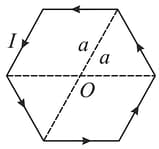
The magnitude of the magnetic field at $O$ is

A long hollow cylindrical metal tube has an inner radius $R$ and outer radius $2R .$ A current I flows along the length of the tube and is uniformly distributed along the cross section of the tube. The length of the tube is much greater than $2R$. If $r$ denotes the distance from the axis of the cylinder, then the magnitude of the magnetic field in the hollow part of the tube $(0<r<R)$ is approximately

Ampere's law is analogous to

A long straight wire of radius $a$ carries a steady current $i.$ The current is uniformly distributed across its cross-section. The ratio of the magnetic field at $\frac{a}{2}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d} 2a$ is

Choose the incorrect option-

The two ends of $\mathrm{a}$ non-conducting spring of force constant $50{\mathrm{Nm}}^{-1}$ and unstretched length of $2 \mathrm{cm}$ are connected to the mid points of two straight parallel rods each of length $4 \mathrm{m}$. When $100 \mathrm{A}$ current is passed through each rod in the same direction, the work done on the spring in $\mathrm{mJ}$ is

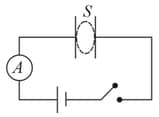
Switch is closed at $t=0.$ At time $t$ suppose current through the ammeter is $i$ then the value of the line integral $\oint \overrightarrow{B}·\overrightarrow{d\ell }$ along the planar loop $S$ drawn in the space between the plates of the capacitor parallel to the plates is given as

STATEMENT-1: A uniformly distributed direct current flows through a solid long metallic cylinder along its length. The magnetic field produced by this current is only outside the cylinder.

STATEMENT- 2: A thin long cylindrical tube carrying uniformly distributed direct current along its length does not produce a magnetic field inside it. Moreover, a solid cylinder can be supposed to be made up of many thin cylindrical tubes.

Ampere’s circuit law is given by

Ampere circuital equation for given problem is equal to

The statement that "the line integral of the tangential component of the magnetic field strength around a closed path is equal to ${\mu }_o$ times the current enclosed by a path" represents

An infinitely long hollow conducting cylinder with inner radius $\frac{R}{2}$ and outer radius $\mathrm{R}$ carries a uniform current density along its length. The magnitude of the magnetic field, $\left|\mathrm{B}\right|$ as a function of the radial distance $\mathrm{r}$ from the axis, is best represented by

Maxwell's modification of Ampere's circuital law is

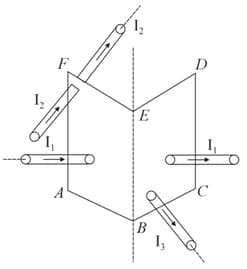
The figure shown, has three long straight current-carrying conductors having current $I_1, I_2 \text{and} I_3$ respectively. Then the value of $\underset{ABCDEFA}{\oint } \overrightarrow{B}·\mathrm{d}\overrightarrow{l}$ will be

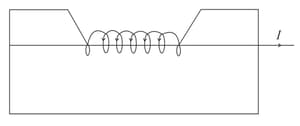
In the diagram shown, a wire carries a current I. What is the value of the $\oint \overrightarrow{B}.\overrightarrow{dl}$ (as in Ampere's law) on the helical loop shown in the figure? The integration is done in the sense shown. The loop has N turns and part of the helical loop on which arrows are drawn is outside the plane of the paper.

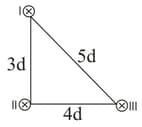
Three long wires, each carrying current $i$ are placed parallel to each other. The distance between I and II is 3d, between II and III is 4d and between III and I is 5d. Magnetic field at the position of wire II is