Biot-Savart’s Law and Its Applications

Biot-savarts law does a common alteration of-

Two very long straight parallel wires, parallel to $y$-axis, carry currents $4I$ and $I$, along $+y$-direction and $-y$-direction, respectively. The wires pass through the $x$-axis at the points $(d, 0, 0)$ and $(-d, 0, 0)$ respectively. The graph of magnetic field $z$-component as one moves along the $x$-axis from $x=-d$ to $x=+d$, is best given by

Equal current i is flowing in three infinitely long wires along positive x, y and z directions. The magnitude field at a point (0, 0, -a) would be:

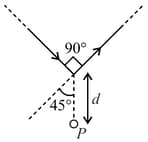
Find the magnetic field at $P$ due to the arrangement shown.

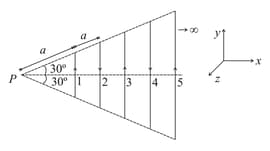
Infinite number of straight wires each carrying current I are equally placed as shown in the figure. Adjacent wires have current in opposite direction. Net magnetic field at point P is.

Two mutually perpendicular conductors carrying currents $I_1 \text{and} I_2$ respectively, lie in one plane. Locus of the point at which the magnetic induction is zero, is a:

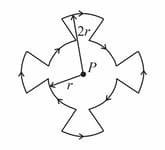
A current I flows around a closed path in the horizontal plane of the circle as shown in the figure. The path consists of eight arcs with alternating radii r and 2r. Each segment of arc subtends equal angle at the common centre P. The magnetic field produced by current path at point P is

Two concentric coils $X$ and $Y$ of radii $16 \mathrm{cm}$ and $10 \mathrm{cm}$ lie in the same vertical plane containing $N-S$ direction. $X$ has $20$ turns and carries $16 \mathrm{A}$. $Y$ has $25$ turns & carries $18 \mathrm{A}$. $X$ has current in anticlockwise direction. The magnitude of net magnetic field at their common centre is-

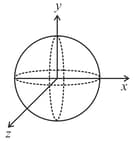
Three rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring then the magnitude of the magnetic field at the common centre is

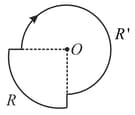
A current of $i$ ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field ${\rm O}$ is,

An infinitely long conductor $PQR$ is bent to form a right angle as shown. A current $I$ flows through $PQR$. The magnetic field due to this current at the point $M$ is ${\mathit{\text{H}}}_1$. Now, another infinitely long straight conductor $QS$ is connected at $Q$ so that the current in $PQ$ remaining unchanged. The magnetic field at $M$ is now ${\mathit{\text{H}}}_2$. The ratio $\frac{H_1}{H_2}$ is,

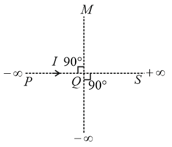
Two coils each of 100 turns are held such that one is in horizontal plane and other in vertical one with their centres coinciding. The radius of the vertical coil is 20 cm and that of the horizontal coil is 30 cm. How would you neutralize the magnetic field of the earth at their common centre? What is the current to be passed through each coil? Horizontal of earth's magnetic induction = 3.49 × 10⁻⁵ T and angle of dip = 30^o. To neutralise the magnetic field at the centre of the coil, the currents is horizontal coil $i_1$ in vertical coil $i_2$  are
 

Three infinitely long thin wires each carrying current $i$ in the same direction, are in the x-y plane a gravity-free space. The central wire is along the y-axis while the other two are along $x=\mp d$ Find the locus of the points for which the magnetic field B is zero.

A ring of the radius $R$ is placed in the $y-z$ plane and it carries a current $i$. The conducting wires which are used to supply the current to the ring can be assumed to be very long and are placed as shown in the figure. The magnitude of the magnetic field at the centre of the ring $\mathrm{A}$ is

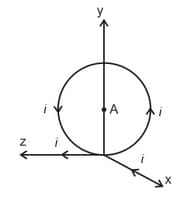
Find the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.

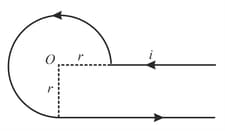
Find the magnetic induction at point $O$, if the current carrying wire is in the shape shown in the figure.

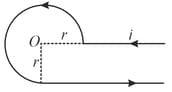
Find the magnetic induction at the origin in the figure shown.

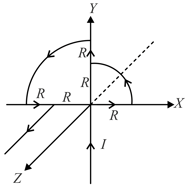
Find the magnetic induction at the origin in the figure shown.

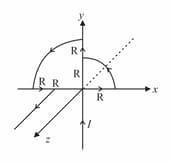
Find the magnetic field at the centre P of square of side a shown in figure.

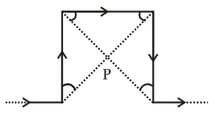
Two circular coils A and B of radius $\frac{5}{\sqrt{2}}$ cm and 5 cm respectively current 5 Amp. and $\frac{5}{\sqrt{2}}$ Amp. respectively. The plane of B is perpendicular to plane of A their centres coincide. Find the magnetic field at the centre.