Solenoid and Toroid

Using Ampere’s circuital law,obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.

A toroid of $n$ turns, mean radius $R$ and cross-sectional radius $a$ carries current $I.$ It is placed on a horizontal table taken as $xy$-plane. Its magnetic moment m _______

The magnetic field inside a long solenoid is

A long solenoid contains another coaxial solenoid whose radius $R$ is half of its own. Their coils have the same number of turns per unit length and initially both carry no current. At the same instant current start increasing linearly with time in both solenoid. At any moment the current flowing in the inner coil is twice as large as that in the outer one and their directions are the same. The ratio of the magnetic field at $r<R$ to $R<r<2 R$ is :

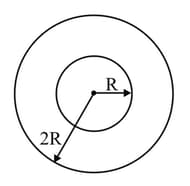
When the number of turns in a toroidal coil is doubled, then the value of magnetic flux density will become,

A short solenoid (length $l$ and radius $r$ with $n$ turns per unit length) lies well inside and on the axis of a very long, coaxial solenoid (length $L$, radius $R$ and $N$ turns per unit length, with $R>r$). Current $I$ follows in the short solenoid. Choose the correct statement.

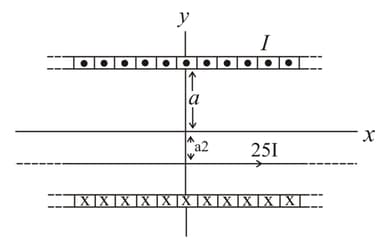
An infinitely long solenoid of radius a $=\frac{5}{\pi }\mathrm{cm}$ and $10 \mathrm{turns} {\mathrm{cm}}^{-1}$ is placed such that its axis of symmetry lies along the $X$-axis. A current $I$ is flowing through the solenoid ( $X$ means that $I$ is flowing into and $·$ means it is flowing out of the page). A straight infinite wire with current $25 I$ is placed parallel to the $X-$axis at a distance $\frac{a}{2}$ away from the center. Which of the following gives the direction of net magnetic field at the origin?

A long solenoid has $200$ turns per cm and carries a current $i$. The magnetic field at its centre is $6.28\times {10}^{-2} \mathrm{Wb} {\mathrm{m}}^{-2}$. Another long solenoid has $100$ turns per $\mathrm{cm}$ and it carries a current $\frac{i}{3}.$ The value of the magnetic field at its centre is $\alpha \times {10}^{-2} \mathrm{Wb} {\mathrm{m}}^{-2}.$ Write the value of $\left[\alpha \right],$ where $\left[ \right]$ is the greatest integer function.

A long solenoid has six layers of windings of $450$ turns each. If diameter is $2.2 \mathrm{cm}$, length is $90 \mathrm{cm}$ and current carried is $6 \mathrm{A}$, then calculate the magnitude of magnetic field inside the solenoid.

Calculate the magnitude of magnetic induction at one end of a solenoid of $100$ turns and total length $50 \mathrm{cm}$ if it carries a current of $2.5 \mathrm{A}$.

Two current-carrying solenoids exhibit: 

A tightly wound solenoid of radius $‘a’$ and length $‘l’$ has $n$ turns per unit length. It carries an electric current $i$. Magnetic field at a distance $\frac{l}{4}$ from one of the end (inside the solenoid on its axis) is $B=\frac{{\mu }_{0}ni\left(\sqrt{5}+3\right)}{\sqrt{K}}$ for $l=4a$ . Find the value of $K$.

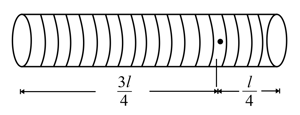
A solenoid of $2.5 \mathrm{m}$ length and $2.0 \mathrm{c}\mathrm{m}$ diameter possesses $10$ turns per cm. A current of $0.5 \mathrm{A}$ is flowing through it. The magnetic induction at axis inside the solenoid is

A long solenoid is fabricated to closely winding wire of radius $0.5 \mathrm{m}\mathrm{m}$ over a cylindrical frame, so that the successive turns nearly touch each other. The magnetic field at the centre of solenoid, if it carries a current of $5 \mathrm{A}$ is.

The turns of a solenoid, designed to provide a given magnetic flux density along its axis, are wound to fill the space between two concentric cylinders of fixed radii. How should the diameter $d$ of the wire used be chosen so as to minimize the heat dissipated in the windings?

An iron ring of relative permeability has windings of insulated copper wire of n turns per metre. When the current in the windings is I, find the expression for the magnetic field in the ring. (b)Identify the type of magnetic material. Draw the modification of the field pattern on keeping a piece of this material in a uniform magnetic field.

A solenoid of length 1.0m has a radius of 1cm and has a total of 1000 turns wound on it. It carries a current of 5A. If an electron were to move with a speed of ${10}^4 m{s}^{-1}$ along the axis of this current carrying solenoid the force experienced by this electron is

If B and E denote induction of magnetic field and energy density at the mid-point of a long solenoid carrying a current I, then which of the following graph is correct-

Field inside a solenoid is -

Two coaxial long solenoids of equal lengths have currents ${\mathrm{i}}_1$ and ${\mathrm{i}}_2$, the number of turns per unit length ${\mathrm{n}}_1$ and ${\mathrm{n}}_2$ and radii ${\mathrm{r}}_1$ and ${\mathrm{r}}_2$ $\left[{\mathrm{r}}_2>{\mathrm{r}}_1\right]$ respectively. If ${\mathrm{n}}_1{\mathrm{i}}_1={\mathrm{n}}_2{\mathrm{i}}_2$ and the two solenoids carry currents in the opposite sense, the magnetic energy stored per unit length is