Cyclotron

In cyclotron, radius of circular path traced by positive ions is_____

A Cyclotron is used to accelerate _____

Cyclotron does not accelerate electron because mass of the electron is very small.

Calculate the magnetic field in which the cyclotron dees should be placed to accelerate protons. The applied frequency is $8$ megacycles/second. Take proton mass $1.67 \mathrm{x} {10}^{-27} \mathrm{kg}.$

What is the use of a cyclotron?

Cyclotron works on the principle that a charged particle moving parallel to the magnetic field experiences a magnetic force and particle moves in circular path.

A cyclotron is used to accelerate protons to a kinetic energy of $5 \mathrm{MeV}$. If the strength of magnetic field in the cyclotron is $2T$, Magnitude of radius and the frequency needed for the applied alternating voltage of the cyclotron is
(Given: Velocity of proton $=3\times {10}^7 \mathrm{m}/\mathrm{s}$).

Write some of the applications of a cyclotron.

A cyclotron is operating at a frequency of $12 \mathrm{MHz}$. Mass and charge of deuteron are $3.3\times {10}^{-27} \mathrm{kg}$ and $1.6\times {10}^{-19} \mathrm{C}$. To accelerate deutron, the necessary magnetic field is

A cyclotron is operating at a frequency of $12 \mathrm{MHz}$. Mass and charge of deuteron are $3.3\times {10}^{-27} \mathrm{kg}$ and $1.6\times {10}^{-19} \mathrm{C}$. To accelerate deuteron, the necessary magnetic field is

Describe the construction of cyclotron and explain its principle of action.

What is cyclotron? State its principle.

Radius of "Dee" of cyclotron is $0.5 \mathrm{m}$. A magnetic field of $1.7 \mathrm{T}$ is perpendicular to it. Find the maximum energy gained by proton.

A proton of energy $100 \mathrm{eV}$ is moving in circular path in perpendicular magnetic field of ${10}^{-4} \mathrm{T}$. The cyclotron frequency of the proton in $\raisebox{1ex}{$\mathrm{radian}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{s}$}\right.$  will be

A cyclotron is a device for accelerating ions and charged particles. It was developed by Lawrence in $1932$ .The heart of the apparatus consists of a split metal pillbox. Figure shows top and front views of the halves called Dees. A rapidly oscillating potential difference is applied between the Dees. This produces an oscillating electric field in the gap between the Dees, the region inside each Dee being essentially free of electric field. The Dees are enclosed in an evacuated container, and the entire unit is placed in a uniform magnetic field $B$ whose direction is normal to the plane of Dees, A charged particle of mass $\text{'}m\text{'}$ and charge $\text{'}q\text{'}$ in the gap between the Dees is accelerated by the electric field towards one of them. Inside the Dees, it moves with constant speed in a semi-circle.

The period of uniform circular motion is $T\mathit{=}\frac{\mathit{2}\pi m}{qB}$ and is independent of speed. If the time period of the oscillating electric field is equal to this time, then the charged particle will be accelerated again and again.

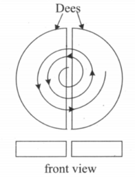
Answer the following questions (consider the mass of particles remains constant during motion):

A cyclotron has been adjusted to accelerate deuterons. It is now to be adjusted to accelerate other particles. Which of the following changes may be made for this?

$\left(\mathrm{a}\right)$ In order to keep the frequency of oscillating electric field same, the magnetic field is halved for proton.

$\left(\mathrm{b}\right)$ If the magnetic field remains unchanged, the oscillation frequency of electric field should be halved for $\alpha$-particle.

$\left(\mathrm{c}\right)$ If the magnetic field remains unchanged, the oscillation frequency of electric field should be doubled for proton.

$\left(\mathrm{d}\right)$ If the frequency of oscillating electric field is kept same, the magnetic field should be kept same for $\alpha$-particle.

A cyclotron is accelerating deuterons having mass$=2\times 1.6\times {10}^{-27} \mathrm{kg}$, charge $\mathit{+}e$, in the magnetic field $B=2 \mathrm{T}$. If the deuterons are to acquire $100 \mathrm{MeV}$ of kinetic energy and the difference of potential across the gap is $20 \mathrm{kV}$, the number of passes through the electric field will be

A cyclotron is accelerating deuterons having mass $2\times 1.6\times {10}^{-27} \mathrm{kg}$, charge $+e$ and $B=2 \mathrm{T}$. The maximum radius of the Dees required, if deuteron is to acquire $100 \mathrm{MeV}$ of energy, is

A proton is accelerating on a cyclotron having oscillating frequency of $11 \mathrm{MHz}$in external magnetic field of $1 \mathrm{T}$. If the radius of its dees is $55 \mathrm{cm}$, then its kinetic energy (in $\mathrm{MeV}$) is ( $m_{\mathrm{p}}=1.67\times {10}^{-27}\mathrm{ }\mathrm{k}\mathrm{g},\mathrm{ }e=1.6\times \mathrm{ }{10}^{-19}\mathrm{ }\mathrm{C}$ )

An electron is moving in a cyclotron at a speed of $3.2\times {10}^7\mathrm{ }\mathrm{m} {\mathrm{s}}^{-1}$ in a magnetic field  $5\times {10}^{-4} \mathrm{T}$ perpendicular to it. The frequency of this electron is:$\left(q=1.6\times {10}^{-19}\mathrm{ }\mathrm{C},\mathrm{ }{m}_{\mathit{e}}=9.1\times {10}^{-31}\mathrm{ }\mathrm{k}\mathrm{g}\right)$

The operating magnetic field for accelerating protons in a cyclotron oscillator having frequency of $12\mathrm{ }\mathrm{M}\mathrm{H}\mathrm{z}$ is:$\left(\mathrm{q}=1.6\times {10}^{-19}\mathrm{ }\mathrm{C},\mathrm{ }{\mathrm{m}}_{\mathrm{p}}=1.67\times {10}^{-27}\mathrm{k}\mathrm{g}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }1\mathrm{ }\mathrm{M}\mathrm{e}\mathrm{V}=1.6\times {10}^{-13}\mathrm{J}\mathrm{ }\right)$