Magnetic Field on the Axis of a Circular Current Loop

Find out the expression for the magnetic field at a point on the centre of a coil of radius carrying current I and having N number of turns.

What is the magnetic field at the centre of the current-carrying loop?

The magnitude of a magnetic field at the centre of a circular coil of radius $R$ , having $N$ turns and carrying a current $I$ can be doubled by changing

The magnetic field normal to the plane of $\mathrm{a}$ coil of $n$ turns and radius $r$ carrying $\mathrm{a}$ current $i$ is measured on the axis of the coil at $\mathrm{a}$ distance $h$ $\left(\mathrm{h}<<\mathrm{r}\right)$ from the centre of the coil. This is smaller than the field at the centre by the fraction

Two concentric coplanar circular loops of radia $r_1$ and $r_2$ cary currents $i_1$ and $i_2$ respectively, in opposite directions ($i_1$ clockwise and $i_2$ anticlockwise.) The magnetic induction at the centre of the loops is half of that due to $i_1$ alone at the centre. If $r_2=2r_1$, the value of $i_2/i_1=$

The surface charge density of a thin charged disc of radius $R$ is $\sigma .$ The value of the electric field at the centre of the disc is $\frac{\sigma }{2{\in }_0}$.

With respect to the field at the centre, the electric field along the axis at a distance $R$ from the centre of the disc :

Two identical wires $A$ and $B$, each of length $\text{'}𝑙\text{'}$, carry the same current $I$. Wire $A$ is bent into a circle of radius $R$ and wire $B$ is bent to form a square of side $\text{'}a\text{'}$. If $B_{\mathrm{A}}$ and $B_{\mathrm{B}}$ are the values of the magnetic field at the centres of the circle and square respectively, if the ratio$\frac{B_{\mathrm{A}}}{B_{\mathrm{B}}}$ is $\frac{{\mathrm{\pi }}^2}{ N\sqrt{2}}$ then the value of $N$ is :

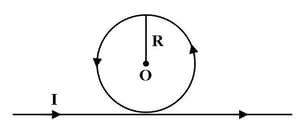
An infinitely long straight conductor is bent into the shape as shown below. It carries a current of $I$ ampere and the radius of the circular loop is $R$ metre. Then, the magnitude of magnetic induction at the centre of the circular loop is -

A current loop consists of two identical semicircular parts each of radius $R$, one lying in the x-y plane and the other in x-z plane. If the current in the loop is $i$, The resultant magnetic field due to the two semicircular parts at their common centre is

A straight conductor of length $l$ carrying a current $I,$ is bent in the form of a semicircle. The magnetic field (in tesla) at the centre of the semicircle is

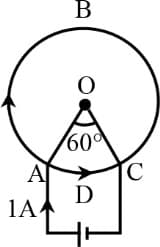
A cell is connected between the points $A$ and $C$ of a circular conductor $ABCD$ with $O$ as centre and angle $AOC=60°$. If $B_1$ and $B_2$ are the magnitudes of the magnetic fields at $O$ due to the currents in $ABC$ and $ADC$ respectively, then ratio $\frac{B_1}{B_2}$ is

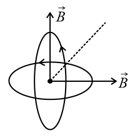
Two circular current coils are concentric and their planes are mutually perpendicular and the magnetic field due to each coil is $B$, as shown in the figure: the net magnetic field at their common center will be

Calculate the intensity of magnetic induction at distance $x$ from the centre $(x>>R)$ of a circular coil of radius $R$ carrying a current of $I$.

A circular coil of two turns produces a magnetic field of $0.2 \mathrm{T}$ at its centre.If this same coil is rewound into a circular coil of four turns keeping the current constant, then calculate the new value of magnetic field at the centre of the coil.

What will be the current flowing in a tightly wound $90$ turn coil of radius $15 \mathrm{cm}$, if it is known that the magnetic field at its centre is $4\times {10}^{-4} \mathrm{T}$?

Calculate the magnitude of magnetic field at the centre of a $100$ turn circular coil of radius $9 \mathrm{cm}$, if it carries a current of $0.4 \mathrm{A}$.

Two circular coils $\mathrm{X}$ and $\mathrm{}\mathrm{Y}$, having equal number of turns and carrying current in the same sense. Subtend same solid angle at point $\mathrm{O}$ if the smaller coil $\mathrm{X}$ is midway between $\mathrm{O}$ and coil $\mathrm{Y}$. ${\mathrm{B}}_{\mathrm{y}}$ is magnetic fied due to coil $\mathrm{Y}$ and that due to smaller coil $\mathrm{X}$ at $\mathrm{O}$ is ${\mathrm{B}}_{\mathrm{x}},$ then find the ratio $\frac{{\mathrm{B}}_{\mathrm{x}}}{{\mathrm{B}}_{\mathrm{y}}}$

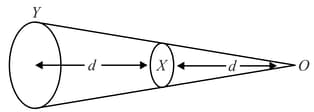
Two circular coil made of similar wires but of radii $20 \mathrm{c}\mathrm{m}$ and $40 \mathrm{c}\mathrm{m}$ are connected in parallel. Find the ratio of the magnetic fields at their centres.

Two wires of same length are bent in the form of a circle and square respectively. If same current

passes in both of then, find the ratio of magnetic fields at their centres

Magnetic field at point O will be