Newton’s Law of Cooling

An object cools from $100°\mathrm{C}$ to $40°\mathrm{C}$ in $10$ minutes, when the surrounding temperature is $10°\mathrm{C}$. Then the time taken by the object to cool from $70°\mathrm{C}$ to $20°\mathrm{C}$ is
[Take $\ln 2=0.7,\ln 3=1.1,\ln 6=1.8$]

A hot container takes $1$ min to cool from $95 °\mathrm{C}$ to $75 °\mathrm{C}$. The time it takes to cool from $74 °\mathrm{C}$ to $54 °\mathrm{C}$ is
[consider the room temperature as $30 °\mathrm{C}$]

A brass boiler has a base area $0.15{\mathrm{m}}^2$ and thickness $1.0\mathrm{cm}.$ It boils water at the rate of $6.0\mathrm{kg}/\min$ when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass:

A body cools down from $80 °\mathrm{C}$ to $60 °\mathrm{C}$  in 10 minutes when the temperature of surrounding is $30 °\mathrm{C}$. The temperature of the body after next 10 minutes will be:

A body cools from $67°\mathrm{C}$ to $37°\mathrm{C}.$ If this takes time $t$ when the surrounding temperature is $27°\mathrm{C},$ what will be the time taken if the surrounding temperature is $7°\mathrm{C} ?$

Two identical beakers $\mathrm{A}$ and $\mathrm{B}$ contain equal volumes of two different liquids at $60°\mathrm{C}$ each and left to cool down. Liquid in $\mathrm{A}$ has density of $8\times {10}^2\mathrm{ }\mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}$ and specific heat of $2000\mathrm{ }\mathrm{J}\mathrm{ }\mathrm{k}{\mathrm{g}}^{-1}{\mathrm{K}}^{-1}$ while the liquid in $\mathrm{B}$ has density ${10}^3\mathrm{ }\mathrm{k}\mathrm{g}{\mathrm{ }\mathrm{m}}^{-3}$ and specific heat of $4000 \mathrm{J}\mathrm{ }\mathrm{k}{\mathrm{g}}^{-1}{\mathrm{K}}^{-1}$. Which of the following best describes their temperature versus time graph schematically? (assume the emissivity of both the beakers to be the same)

If a piece of metal is heated to temperature$\mathrm{ \theta }$ and then allowed to cool in a room which is at temperature${\theta }_0$, the graph between the temperature $T$ of the metal and time $t$ will be closest to :

Hot water in a vessel kept in a room, cools from $75°\mathrm{C}$ to $70°\mathrm{C}$ in ${\mathrm{t}}_1$ minutes, from   $70°\mathrm{C}$ to $65°\mathrm{C}$ in ${\mathrm{t}}_2$ ​minutes and from $65°\mathrm{C}$ to $60°\mathrm{C}$ in ${\mathrm{t}}_3$ minutes. Then,

The circuit below is used to heat water kept in a bucket. 

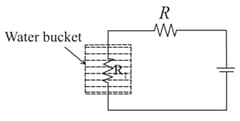
Assuming heat loss only by Newton's law of cooling, the variation in the temperature of the water in the bucket as a function of time is depicted by

A body cools down from $75 °\mathrm{C}$ to $70 °\mathrm{C}$ in time $\left(\Delta t_1\right)$, from $70 °\mathrm{C}$ to $65 °\mathrm{C}$ in time $\left(\Delta t_2\right)$ and $65 °\mathrm{C}$ to $60 °\mathrm{C}$ in time $\left(\Delta t_3\right)$. The correct statement according to Newtons law of cooling is

A cup of tea cools from $80°\mathrm{C}$ to $60°\mathrm{C}$ in one minute. The ambient temperature is $30°\mathrm{C}.$ In cooling from $60°\mathrm{C}$ to $50°\mathrm{C},$ it will take:

A calorimeter of water equivalent $5\times {10}^{-3}\mathrm{kg}$, takes $3 \min$ to cool from ${28}^o\mathrm{C}$ to ${21}^o\mathrm{C}$ having $25\times {10}^{-3}\mathrm{kg}$ of water. It takes $2 \min$ to cool from ${28}^o\mathrm{C}$ to ${21}^o\mathrm{C}$, if it is filled with $30\times {10}^{-3}\mathrm{kg}$ of turpentine oil. Find the specific heat of turpentine oil.

The time required by two liquids to cool from $60 °\mathrm{C}$ to $50 °\mathrm{C}$ is $324 \mathrm{s}$ and $810 \mathrm{s}$, respectively. What is the ratio of densities of these liquids if the ratio of specific heat of both are $3:4$? (water equivalent of the calorimeter is negligible)

It is known for a certain liquid that it takes $70 \mathrm{s}$ to cool from ${55}^{\mathrm{o}}\mathrm{C}$ to ${50}^{\mathrm{o}}\mathrm{C}$ and $30 \mathrm{s}$ to cool from  ${95}^{\mathrm{o}}\mathrm{C}$ to ${90}^{\mathrm{o}}\mathrm{C}$. Figure out the ambient temperature of the room.

Calculate the net rate of radiation loss from a solid cube of side $1 \mathrm{m}$, which has a temperature of ${127}^{\mathrm{o}}\mathrm{C}$ while the ambient temperature is ${27}^{\mathrm{o}}\mathrm{C}$. It is given that the cube has an emissivity of $\frac{1}{5.67}$.

"The rate of loss of heat $-\frac{dQ}{dt}$ of the body is directly proportional to the temperature difference $\mathrm{\Delta }T=(T_2-T_1)$ of the body and surroundings". Choose the correct option related to this statement.

Steel is heated to temperature$\mathrm{ \theta }$ and then allowed to cool in a room which is at temperature${\mathrm{ \theta }}_0$, the graph between the temperature $T$ of steel and time $t$ will be closest to

A body cools in a surrounding of constant temperature $30 °\mathrm{C}$. Its heat capacity is $2 \mathrm{J} °{\mathrm{C}}^{-1}$. The initial temperature of the body is $40 °\mathrm{C}$. Assume Newton's law of cooling is valid. The body cools to $36 °\mathrm{C}$ in $10 \min$. In further $10$ $\min$ it will cool from $36 °\mathrm{C}$ to 

A body cools in $7 \mathrm{m}\mathrm{i}\mathrm{n}$ from ${60}^{\mathrm{ o}}\mathrm{C}$ to ${40}^{\mathrm{ o}}\mathrm{C}.$ What time (in min) does it take to cool from ${40}^{\mathrm{ o}}\mathrm{C}$ to ${28}^{\mathrm{ o}}\mathrm{C},$ if surrounding temperature is ${10}^{\mathrm{ o}}\mathrm{C}?$ (Assume Newton's law of cooling)

A cup of tea cools from ${65.5}^{\mathrm{ o}}\mathrm{C}$ to ${62.5}^{\mathrm{ o}}\mathrm{C}$ in $1\text{min}$ in a room at ${22.5}^{\mathrm{ o}}\mathrm{C}$. How long will it take to cool from ${46.5}^{\mathrm{ o}}\mathrm{C}$ to ${40.5}^{\mathrm{ o}}\mathrm{C}$ in the same room?