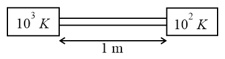Conduction

A metal rod of length $2 \mathrm{m}$ has cross sectional areas $2A$ and $A$ as shown in the figure. The ends are maintained at temperatures $100°\mathrm{C}$ and $70°\mathrm{C}$. The temperature at middle point $C$ is___$°\mathrm{C}$.

How is the microscopic level of energy related to the macroscopic level of energy?

How is heat transferred on the particle level?

What is the description of heat flow?

What is Searle's method for thermal conductivity?

What is heat on a microscopic level?

A copper rod of length $2.5 \mathrm{m}$ and an iron rod of length $1.5 \mathrm{m}$ having the same areas of cross section are connected in series. Thermal conductivities of copper and iron are respectively $400$ and $80$ $\mathrm{SI}$ units. The equivalent conductivity of the composite bar in $\mathrm{SI}$ unit is ____.

Heat is passed through two cylindrical rods of same material. Their diameters and lengths are in the ratio $1:2$ and $2:1$ respectively. If their ends are maintained at same temperature difference, the ratio of rate of flow of heat through them is

What is the rate of flow of heat through a tapering rod of length $\ell$ tapering from radius $r_1$ and $r_2,$ when the temperature of the ends are ${\theta }_1°\mathrm{C}$ and ${\theta }_2{}^{\circ }\mathrm{C}$ and coefficient of thermal conductivity is $\mathrm{K}?$

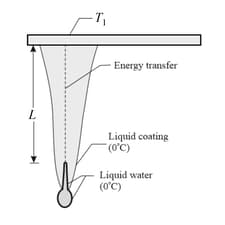
Liquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of $0 °\mathrm{C}$, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions. It can lose energy and freeze only by sending energy up (through distance $L$ ) to the top of the icicle, where the temperature $T_r$ can be below $0 °\mathrm{C}.$ Take $L=0.10 \mathrm{m}$ and $T_r=-5 °\mathrm{C}.$ Assume that the central tube and the upward conduction path both have cross-sectional area $A=0.5 {\mathrm{m}}^2.$ The thermal conductivity of ice is $0.40 \mathrm{W}/\mathrm{m}·\mathrm{K},$ latent heat of fusion is $L_F=4.0\times {10}^5 \mathrm{J}/\mathrm{k}$ and the density of liquid water is $1000 \mathrm{kg}/{\mathrm{m}}^3$.

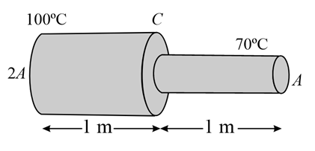
A uniform copper rod $1 \mathrm{m}$ long is insulated on its sides and has the ends exposed to ice and steam respectively. If there is a layer of water $2 \mathrm{mm}$ thick at each end, then what is temperature gradient in the bar ? (Given: Thermal conductivity of copper is $435 {\mathrm{Wm}}^{-1}{\mathrm{K}}^{-1}$ and that of water is $\left.0.435 {\mathrm{Wm}}^{-1}{\mathrm{K}}^{-1}\right)$

One end of a copper rod of uniform cross-section and of length 1.5 m is kept in contact with ice and the other end with water at 100^oC. At what point along its length should a temperature of 200^oC be maintained so that in steady state, the mass of ice melting be equal to that of the steam produced in the same interval of time? Assume that the whole system is insulated from the surroundings. Latent heat of fusion of ice and vaporisation of water are 80 cal/g and 540 cal/g respectively.

Two insulated metal bars each of length $5 \mathrm{c}\mathrm{m}$ and rectangular cross-sections with sides $2 \mathrm{c}\mathrm{m}$ and $3 \mathrm{c}\mathrm{m}$ are wedged between two walls, one held at $100°\mathrm{C}\mathrm{}$ and the other at $0°\mathrm{C}$. The bars are made of lead and silver. $K_{\mathrm{P}\mathrm{b}}=350 \mathrm{W} {\mathrm{m}}^{-1} {\mathrm{K}}^{-1}, K_{\mathrm{A}\mathrm{g}}=425 \mathrm{W} {\mathrm{m}}^{-1} {\mathrm{K}}^{-1}$

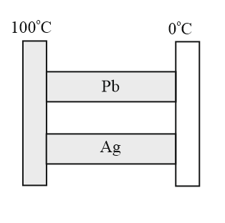
Thermal current through lead bar is

Radius of a conductor increases uniformly from left end to right end as shown in figure.

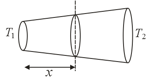
Material of the conductor is isotropic and its curved surface is thermally isolated from surrounding. Its ends are maintained at temperatures ${\mathrm{T}}_1$ and ${\mathrm{T}}_2({\mathrm{T}}_1>{\mathrm{T}}_2)$. If, in steady state, heat flow rate is equal to $\mathrm{H}$, then which of the following graphs is
correct?

Pouring warm water into a thick glass tumbler can crack it because

A cubical thermocol ice box of side $20 \mathrm{cm}$ has a thickness $5 \mathrm{cm}$. If $5\mathrm{ }\mathrm{k}\mathrm{g}$ of ice is put in the box, the amount of ice remaining after $10$ hours is (The outside temperature is $50 \mathrm{℃}$ and the coefficient of thermal conductivity of the thermocol $=0.01\mathrm{ }\mathrm{J} {\mathrm{s}}^{-1} {\mathrm{m}}^{-1} {\mathrm{℃}}^{-1},$ latent heat of fusion of ice $=335\times {10}^3\mathrm{ }\mathrm{J} \mathrm{k}{\mathrm{g}}^{-1}$)

Two rods of equal length and diameter have thermal conductivities $3$ and $4$ units respectively. If they are joined is series, the thermal conductivity of the combination would be:

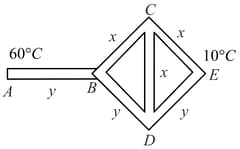
Three rods of material $x$ and three rods of material $y$ are connected as shown in diagram ($a$). All the rods are of identical length and cross-sectional area. If the end $A$ is maintained at $60°\mathrm{C}$ and the junction $E$ at $10°\mathrm{C}$, calculate the temperature of junction $C$. The thermal conductivity of $x$ is $0.92 \mathrm{cal} {\mathrm{cm}}^{-1} {\mathrm{s}}^{-1} °{\mathrm{C}}^{-1}$ and that of $y$ is $0.46 \mathrm{cal} {\mathrm{cm}}^{-1} {\mathrm{s}}^{-1} °{\mathrm{C}}^{-1}$. If your answer is $4n°\mathrm{C}$, then what is the value of $n$?

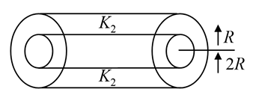
A cylinder has an inner radius $R$ and outer radius $2R.$ The inner part is filled with a material of conductivity $K_1$ and outer with $K_2$ . Find the equivalent thermal conductivity of the cylinder.

A Copper rod of length $1$ meter and conductivity $K=0.1J/m$ - $K$ is maintained at temperature ${10}^{2}K$ and ${10}^{3}K$ at its ends. The energy flux inside the rod in thermal equilibrium is.