Collisions

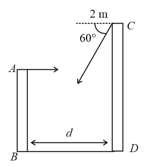
Two towers $AB$ and $CD$ are situated a distance $d$ apart as shown in figure. $AB$ is $20 \mathrm{m}$ high and $CD$ is $30 \mathrm{m}$ high from the ground. An object of mass $m$ is thrown from the top of $AB$ horizontally with a velocity of $10$ $\mathrm{m}{\mathrm{s}}^{-1}$  towards $CD$. Simultaneously another object of mass $2m$ is thrown from the top of $CD$ at an angle of $60°$ to the horizontal towards $AB$ with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other. Find the position where the objects hit the ground (from $B$).

A small block of mass $M$ moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from ${60}^{\circ }$ to ${30}^{\circ }$at point B. The block is initially at rest at A. Assume that collisions between the block and incline are totally inelastic. 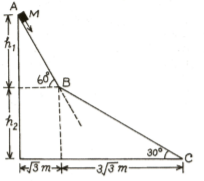$\left(g=10 \mathrm{m}/{\mathrm{s}}^2\right)$. 

A block of mass $0.50 \mathrm{kg}$ is moving with a speed of $2.00 \mathrm{m} {\mathrm{s}}^{-1}$ on a smooth surface. It strikes another mass of $1.00 \mathrm{kg}$ and then they move together as a single body. The energy loss during the collision is:

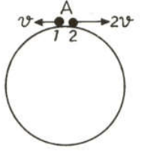
Two small particles of equal masses start moving in opposite directions from a point $A$ in a horizontal circular orbit. Their tangential velocities are $v$ and  $2 v$, respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many collisions, other than that at $A$, these two particles will again reach the point $A$?

A smooth sphere $A$ is moving on a frictionless horizontal plane with angular speed $\omega$ and centre-of- mass velocity $v$. It collides elastically and head-on with an identical sphere $B$ at rest. Neglect friction everywhere. After collision, their angular speeds are ${\omega }_A$ and ${\omega }_B$ respectively. Then:

Consider a rubber ball freely falling from a high height  $h = 4.9 \mathrm{m}$on to a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be:

Two particles of masses $m_1$ and $m_2$, in projectile motions, have velocities $v_1<v_2$ respectively at $t=0$. They collide at time $t_0$. The velocities become $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$ at time $2t_0$ while moving in air. The value of $\left[\left(m_1\overrightarrow{v_1}+m_2{\overrightarrow{v}}_2\right)-\left(m_1\overrightarrow{v_1}+{\mathrm{m}}_2{\overrightarrow{v}}_2\right)\right]$ is

A point mass of $1 \mathrm{kg}$ collides elastically with a stationary point mass of $5 \mathrm{kg}$. After their collision, the $1 \mathrm{kg}$ mass reverses its direction and moves with a speed of $2 \mathrm{m} {\mathrm{s}}^{-1}$. Which of the following statements is correct for a system of these two masses?

Two objects of the same mass and with the same initial speed, moving in a horizontal plane, collide and move away together at half their initial speeds after the collision. The angle between the initial velocities of the objects is,

Two masses $\mathrm{m}$ and $2\mathrm{m}$ are placed in a fixed horizontal circular smooth hollow tube as shown. The mass $\mathrm{m}$ is moving with speed $\mathrm{u}$ and the mass $2\mathrm{m}$ is stationary. After their first collision, the time elapsed for next collision is (Coefficient of restitution is, $\mathrm{e}=\frac{1}{2}$)

A particle of mass $m_1$ and velocity $v_{\mathrm{i}}$ collides head-on with a stationary particle of mass $m_2$. After collision the velocity of both particles is $v_{\mathrm{j}}$. The energy lost in the collision is:

A proton of mass $1$ a.m.u. collides with a Carbon-$12$ nucleus (mass = $12$ a.m.u.) at rest. Assuming that the collision is perfectly elastic and that the Newton's laws of motion hold, what fraction of the proton's kinetic energy is transferred to the Carbon nucleus ?

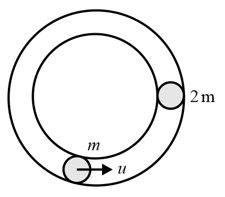
Two identical spheres $\mathrm{P}$ and $\mathrm{Q}$ lie on a smooth horizontal circular groove at opposite ends of a diameter. $\mathrm{P}$ is projected along the groove and at the end of time $t$, impinges on $\mathrm{Q}$. If $e$ is the coefficient of restitution, then the second impact will occur after the shortest time of

A tennis ball is released from height $h$ above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after the third collision, $e$ is the coefficient restitution between ball and ground?

A body of mass $m_1$ moving with an unknown velocity of $v_1 \hat{\mathrm{i}},$ undergoes a collinear collision with a body of mass $m_2$ moving with a velocity $v_2 \hat{\mathrm{i}}.$ After the collision, $m_1$ and $m_2$ move with velocities of $v_3\mathrm{ }\hat{\mathrm{i}}$ and $v_4\mathrm{ }\hat{\mathrm{i}},$ respectively. If $m_2=0.5\mathrm{ }{m}_1$ and $v_3=0.5 v_1,$ then $v_1$ is:

A metal ball falls from a height of $1 \mathrm{m}$ on to a steel plate and jumps up to a height of $81 \mathrm{cm}$. The coefficient of restitution of the ball and steel plate is

A smooth sphere $A$ is moving on a frictionless horizontal plane with angular speed $\omega$ and centre of mass velocity $v$. It collides elastically and head-on with an identical sphere $B$ at rest. Neglect friction everywhere. After the collision, their angular speeds are ${\omega }_A$ and ${\omega }_B$ respectively. Then,

When two bodies collide elastically, the force of interaction between them is

Coefficient of restitution during the collision is changed to $\frac{1}{2},$ keeping all other parameters unchanged. What is the velocity of the ball $\mathrm{B}$ after the collision?

A sphere having mass $m$ moving with a constant velocity hits another stationary similar sphere. If $e$ is the coefficient of restitution, then ratio of speed of the first sphere to the speed of the second sphere after collision will be: