Two-Block Problems

Two blocks connected by a massless string slide down an inclined plane having an angle of inclination of  $37°.$  The masses of the two blocks are  $M_1=4kg$  and  $M_2=2kg$  respectively and the coefficients of friction of  $M_1$ and  $M_2$ with the inclined plane are 0.75 and 0.25 respectively. Assuming the string to the taut, find the tension in the string.  $\left(\sin 37°=0.6,\cos 37°=0.8\right)$

Two blocks connected by a massless string slide down an inclined plane having an angle of inclination of $37°.$ The masses of the two blocks are $M_1=4 \mathrm{kg}$ and $M_2=2 \mathrm{kg}$ respectively and the coefficients of friction of $M_1$ and $M_2$ with the inclined plane are $0.75$ and $0.25$ respectively. Assuming the string to be taut, find the common acceleration of two masses. $\left(\sin 37°=0.6, \cos 37°=0.8\right)$

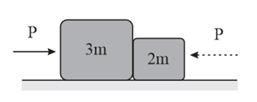
Two blocks of masses $M=5 \mathrm{kg}$ and $m=3 \mathrm{kg}$ are placed on a horizontal surface as shown in fig. The coefficient of friction between the blocks is $0.5$ and that between the block $M$ and the horizontal surface is $0.7$. What is the maximum horizontal force $F$ that can be applied to block $M$ so that the two blocks move without slipping ? Take $g=10 \mathrm{m}/{\mathrm{s}}^2$

Blocks $A$ and $B$ are arranged as shown in the figure. The pulley is frictionless. The mass of $A$ is $10 \mathrm{kg}$. The coefficient of friction between the block $A$ and the horizontal surface is $0.20$. The minimum mass of $B$, to start the motion, will be

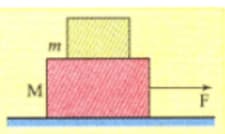
A block of mass $m=2 \mathrm{kg}$ is placed on a plank of mass $\mathrm{M}=10 \mathrm{kg},$ which is placed on a smooth horizontal plane, as shown in the figure. The coefficient of friction between the block and the plank is $\mu =\frac{1}{3}.$ If a horizontal force $F$ is applied on the plank, then the maximum value of $F$ for which the block and the plank move together is $\left(\mathrm{g}=10 \mathrm{m}/{\mathrm{s}}^2\right)$

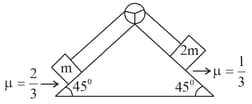
In the arrangement shown in the figure, if the blocks of masses $m$ and $2 \mathrm{m}$ are released from the state of rest, tension in the string is ($\mu =$ coefficient of friction, string is massless and inextensible, pulley is frictionless)

In the situation shown, the reading of the spring balance is $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

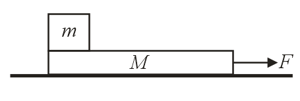
Block 1 sits on top of block $2$. Both of them have a mass of $1$ $\mathrm{kg}$. The coefficients of friction between blocks $1$ and $2$ are ${\mu }_{\mathrm{s}}=0.75$ and ${\mu }_{\mathrm{k}}=0.60$. The table is frictionless. A force $\frac{P}{2}$ is applied on block $1$ to the left, and force $P$ on block $2$ to the right. Obtain the minimum value of $P=P_{\min }$ such that both blocks move relative to each other and fill $\frac{P_{\min }}{2}$ in OMR.

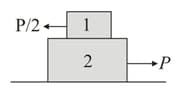
If $F$ force is applied to $10 \mathrm{kg}$ block as shown in diagram then maximum value of $F$ so that there is no relative motion between the blocks.

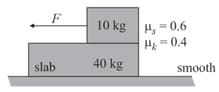
Calculate the accelerations of the blocks $A$ and $B:-$

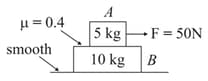
A force of $0.5 \mathrm{N}$ is applied on the upper block as shown in figure. The coefficient of static friction between the two blocks is $0.1$ and that between the lower block and the surface is zero. The work done by the lower block on the upper block for a displacement of $3 \mathrm{m}$ of the upper block is :-

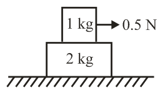
In friction is present between $A \text{\&} B$ only and $F>$ limiting friction between $A\text{ \&} B$. Find acceleration of $A \text{\&} B\mathit{.}$

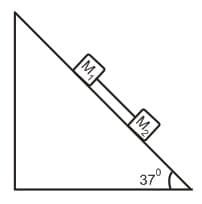
Two blocks connected by a massless string slides down an inclined plane having an angle of inclination of 37°. The masses of the two blocks are M₁ = 4 kg and M₂ = 2 kg respectively and the coefficients of friction of M₁ and M₂ with the inclined plane are 0.75 and 0.25 respectively. Assuming the string to be taut, find the common acceleration of two masses

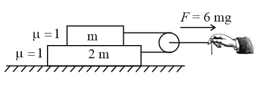
A block of mass $m$ sits on the top of a block of mass $2m$ which sits on a table. The coefficient of kinetic friction between all surface is $\mu = 1$ . A massless string is connected to each mass and wraps halfway around a massless pulley, as shown. Assume that you pull on the pulley with a force of $6mg$. The acceleration of your hand is -

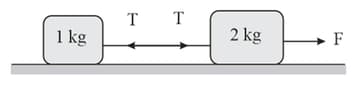
Two blocks masses 1 kg and 2 kg rest on a smooth horizontal table. When the 2 kg block is pulled by a certain force $F$, the tension $T$ in the string is 1.5 N. The value of $F$ is

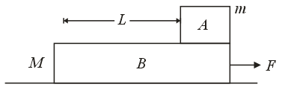
A $40 \mathrm{kg}$ slab rests on a frictionless floor. A $10 \mathrm{kg}$ block rests on top of the slab. The static coefficient of friction between the block and the slab is $0.60$ while the kinetic coefficient of friction is $0.40$. The $10 \mathrm{kg}$ block is acted upon by a horizontal force of $100 \mathrm{N}$. If $g=9.8\mathrm{ }\mathrm{m}{\mathrm{s}}^{-2}$, the resulting acceleration of the slab will be

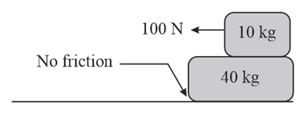
Two blocks of masses $3m$ and $2m$ are in contact on a smooth table. A force $P$ is first applied horizontally on a block of mass $3m$ and then on mass $2 m$. The contact forces between the two blocks in the two cases are in the ratio

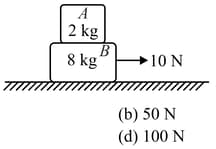
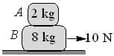
Block $A$ of mass 2 kg is placed over a block $B$ of mass 8 kg. The combination is placed on a rough horizontal surface. If $\mathrm{g}=10\mathrm{m}{\mathrm{s}}^{-2}$, coefficient of friction between $B$ and floor =0.5, coefficient of friction between $A$ and $B$ = 0.4 and a horizontal force of 10 N is applied on 8 kg block, then the force of friction between $A$ and $B$ is

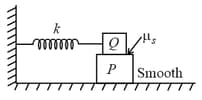
A block $P$ of mass $m$ is placed on a horizontal surface. Another block $Q$ of same mass is kept on $P$ and connected to the wall with the help of a spring of spring constant $k$ as shown in the figure. ${\mathrm{\mu }}_s$ is the coefficient of friction between $P$ and $Q$. The blocks move together performing SHM of amplitude $A$. The maximum value of the friction force between $P$ and $Q$ is

Block $A$ of mass 2 kg is placed over block $B$ of mass 8 kg. The combination is placed over a rough horizontal surface. Coefficient of friction between $B$ and the floor is 0.5. Coefficient of friction between $A$ and $B$ is 0.4. A horizontal force of 10 N is applied on block$B$. The force of friction between $A$ and $B$ is