Kepler's Laws of Planetary Motion

The orbital angular momentum of a satellite is $\mathrm{L}$, when it is revolving in a circular orbit at height $\mathrm{h}$ from earth surface. If the distance of satellite from the earth centre is increased by eight times to its initial value, then the new angular momentum will be

Choose the incorrect statement from the given statements

Duration of a year on a planet is $11$ times of the year on the earth. Find the distance of that planet from the sun. The earth is at distance $1.5\times {10}^8 \mathrm{km}$ from the sun.

A planet is moving in an elliptical path around the Sun. It does obey Kepler's laws of planetary motion. Read the following statements and identify the correct statements
(I) The potential energy of the planet remains same in the entire path.
(II) The kinetic energy of the planet remains same in the entire path.
(III) The total energy of the planet remains same in the entire path.
(IV) The linear momentum of the planet remains same in the entire path.
(V) The angular momentum of the planet remains same in the entire path.

If a planet moving in a circular path having time period of revolution $T$ is suddenly stopped, after what time it will collapse onto the sun?

If a new planet is discovered rotating around the sun with the orbital radius double that of earth, then what will be its time period approximated to the nearest integer (in earth's days)?

(Take $\sqrt{2}=1.414$)

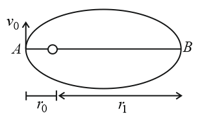
A satellite describes an elliptic orbit about a planet. Denoting by $r_0$ and $r_1,$ the distances corresponding to the perigee and apogee of the orbit. The radius of curvature of the orbit at point $A$ and $B$ in terms of $r_0$ and $r_1$ is $\frac{\alpha r_0{r}_1}{3\left(r_0+r_1\right)}.$ The value of $\alpha$ is.

In an atom, two electrons move around the nucleus in circular orbits of radii $R$ and $4R$. The ratio of the time taken by them to complete one revolution is:

According to Kepler's second law of planetary motion, the areal velocity of a planet revolving around the sun

Assume that the earth moves around the sun in a circular orbit of radius $R$ and there exists a planet which also move around the sun in a circular orbit with an angular speed twice as large as that of the earth. The radius of the orbit of the planet is

The annual variations of solar power incident per unit area at a particular point on the Earth's surface is mainly due to the change in the

Many exoplanets have been discovered by the transit method, where in one monitors, a dip in the intensity of the parent star as the exoplanet moves in front of it. The exoplanet has a radius $R$ and the parent star has radius $100 R$. If $I_0$is the intensity observed on earth due to the parent star, then as the exoplanet transits

A number of planets are revolving around the Sun. Time period is $T$ and average orbital radius of a planet is $R$. A graph is drawn between log $T$ on the $Y-$axis and $\log R$ on the $X-$axis with the origin at $\left(0,0\right)$. The graph is a

The period $T$ and radius $R$ of a circular orbit of a planet about the sun are related by

According to Kepler, the period of revolution of a planet $\left(T\right)$ and its mean distance from the sun $\left(r\right)$ are related by the equation

If $L_1$ and $L_2$ are the angular momenta of two planets of masses $2m$ and $m$ revolving around the sun in circular orbits of radii $r$ and $2r$, then $\frac{L_1}{L_2}$ is

The distances of two planets from the sun are ${10}^{13} \mathrm{m}$ and ${10}^{12} \mathrm{m}$, respectively. The ratio of speeds of two planets around sun is

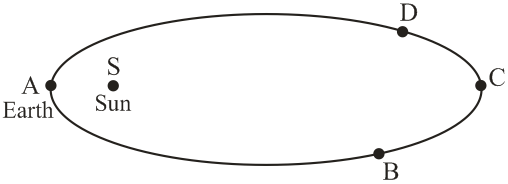
The earth moves in an elliptical orbit with the sun $S$ at one of the foci as shown in the figure. Its kinetic energy is maximum at the point

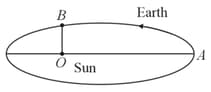
The earth moves around the Sun in an elliptical orbit as shown in figure. The ratio $\mathrm{OA}/\mathrm{OB}=\mathrm{x}.$ The ratio of the speed of the earth at $\mathrm{B}$ to that at $\mathrm{A}$ is nearly

Two planets are moving around the sun. The periodic times and mean radii of the orbits are $T_1, T_2$ and $r_1,r_2$ respectively. The ratio of $T_1/T_2$ is equal to