Motion of Planets and Satellites in Circular Orbits

Satellites $A \text{and }B$ are orbiting around the earth in orbits of ratio $R \text{and} 4R$, respectively. The ratio of their areal velocities is

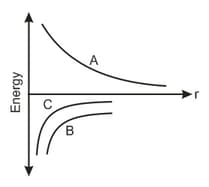
The figure shows the variation of energy with the orbit radius of a body in circular planetary motion. Find the correct statement about the curves A, B and C

A satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passing about a point on the equator is 

Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity  $\frac{{\text{V}}_{\text{A}}}{{\text{V}}_{\text{B}}}\text{is}$

Two spherical stars $A$ and $B$ have densities ${\rho }_A$ and ${\rho }_B$, respectively. $A$ and $B$ have the same radius, and their masses $M_A$ and $M_B$ are related by $M_B=2M_A$. Due to an interaction process, star $A$ loses some of its mass, so that its radius is halved, while its spherical shape is retained, and its density remains ${\rho }_A$. The entire mass lost by $A$ is deposited as a thick spherical shell on $B$ with the density of the shell being ${\rho }_A$. If $v_A$ and $v_B$ are the escape velocities from $A$ and $B$ after the interaction process, the ratio $\frac{v_B}{v_A}=\sqrt{\frac{10n}{{15}^{{\displaystyle \frac{1}{3}}}}}$. The value of $n$ is

A satellite is launched in the equatorial plane in such a way that it can transmit signals up to $60°$ latitude on the earth. The angular velocity of the satellite is $\sqrt{\frac{GM}{n{R}^3}}$. Find $n$.

Assume that there is a tunnel in the shape of a circular arc through the earth. Wall of the tunnel is smooth. A ball of mass ' $m$ ' is projected into the tunnel at A with speed ' $v$ '. The ball comes out of the tunnel at $B$ and escapes out of the gravity of earth. Mass and radius of earth are $M$ and $R$ respectively and radius of circular shaped tunnel is also $R$.

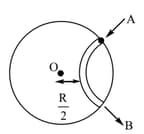
The ratio of $KE$ of a planet at the points $1$ and $2$ is:

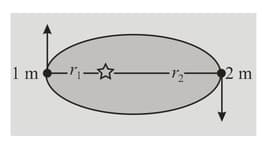
The ratio of $\mathrm{KE}$ of a planet at the points $1$ and $2$ is:

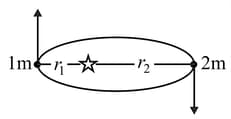
A body of mass $m$ is released from the surface of spherical planet of mass $M$ and radius $R$ having uniform density. The body is constrained to move along a smooth, thin tunnel across the body of planet as shown in figure. Midpoint of the tunnel is at distance of $\frac{R}{2}$ from centre of planet. Then which of the option(s) is/are correct.

A satellite of mass $m$ moves along an elliptical path around a planet of mass $M$, sun being at one of the focus of ellipse. The equation of elliptical path is given by $\frac{x^2}{4}+\frac{y^2}{3}=C^2.$ Then,

A small body of mass $\text{'}m\text{'}$ is projected from the surface of a spherical planet of mass $M$ and radius $R$ with escape velocity in the radially outward direction. Assuming that only gravitational force due to the planet acts on the body during its motion, which of the following options are CORRECT.

A satellite is launched into a circular orbit $1600 \mathrm{km}$ above the surface of the earth. Find the period of revolution in nearest integer (in hours) if the radius of the earth is $R=6400 \mathrm{km}$ and the acceleration due to gravity is (Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ and ${\pi }^2=10$). 

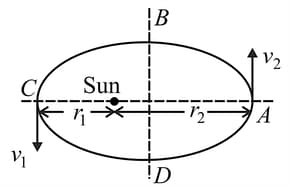
A planet moves around the Sun in an elliptical orbit as shown. Eccentricity of ellipse is $\frac{1}{2}$. Time taken by planet to move from $D$ to $B(D\to A\to B)$ and $B$ to $D$ $(B\to C\to D)$ are respectively $T_{DAB}$ and $T_{BCD}$

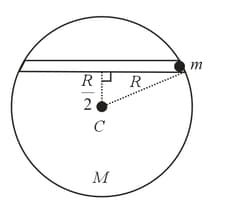
India plans to place geostationary satellites, in equatorial orbit at a height $36000 \mathrm{km}$ from surface of earth. Each of these satellites are arranged equispaced in same orbit and should be able to see each other (exchange signals directly with each other) at any instant of time. If maximum number of such geostationary satellites is $2N+1$1$, then find the value of $N$. (Radius of Earth $=6400 \mathrm{km},{\sin }^{-1}\left(0.15\right)=0.15\mathrm{radian},\pi =3.14$)

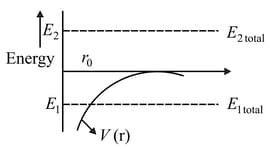
In the graph shown, the $PE$ of earth - satellite system is shown by a solid line as a function of distance $r$ (The separation between earth's centre and satellite). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure by dotted lines.

Based on the above information, answer the following questions.

Mark the correct statement(s).

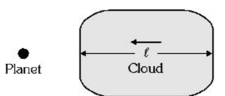
A uniform cloud of dust particles approaches a planet from a great distance with a velocity $v_0$ relative to the planet. Radius of the planet is $R$ and escape velocity from the surface of the planet is $v_{\mathrm{e}}$. Length of the cloud along its direction of motion is $\ell$, cross section of the cloud perpendicular to its direction of motion is very large and its density is $\rho$. How much mass of the dust particles will the planet collect during its passage through the cloud. Mass of the cloud is negligible as compared to the mass of the planet.

Your answer is $\frac{\pi \rho \ell R^{\mathrm{A}}}{B}\left[1+{\left(\frac{v_{\mathrm{e}}}{v_0}\right)}^C\right].$ Find $A+B+C$.

Gravitational acceleration on the surface of a planet is $\frac{\sqrt{6}}{11}g$, where $g$ is the gravitational acceleration on the surface of the earth. The average mass density of the planet is $\frac{2}{3}$ times that of the earth. If the escape speed on the surface of the earth is taken to be $11{\mathrm{kms}}^{-1}$, the escape speed on the surface of the planet in ${\mathrm{kms}}^{-1}$ will be

A satellite $P$ is revolving around the earth at height $h=R$ (Radius of earth) above equator. Another satellite $Q$ is at height $2 h$ revolving in opposite direction it an instant two are at same vertical line passing through center of sphere. Find the least time after which again they are in this situation.

Consider a cylindrical distribution of mass particles around an axis. All particles are identical with the same $\mathrm{K}.\mathrm{E}$ of $K_0$ each to be stable. What is the number density of the particles as a function of radial distance$\left(r\right)$