Average Velocity and Instantaneous Velocity

A particle of mass ${10}^{-2} \mathrm{kg}$ is moving along the positive $\mathrm{x}$-axis under the influence of a force $F\left(x\right)=\frac{-K}{\left(2x^2\right)}$ where $K={10}^{-2}{\mathrm{Nm}}^{-2}$. At time $t=0$ it is at $x=$$1.0 \mathrm{m}$ and its velocity is $v=0$ :
Find the time at which it reaches $x=0.25 \mathrm{m}$

A particle of mass ${10}^{-2} \mathrm{kg}$ is moving along the positive $\mathrm{x}$-axis under the influence of a force $F\left(x\right)=\frac{-K}{\left(2x^2\right)}$ where $K={10}^{-2}N{m}^{-2}.$ At time $t=0$ it is at $x=$$1.0 \mathrm{m}$ and its velocity is $v=0$ :
Find its velocity when it reaches $x=0.50 \mathrm{m}$

The displacement $x$ of particle moving in one dimension, under the action of a constant force is related to the time $t$ by the equation  $t=\sqrt{x}+3$ where $x$ is in meters and $t$ in seconds. Find the displacement of the particle when its velocity is zero.

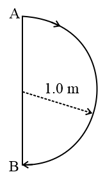
In $1.0 \mathrm{s}$, a particle goes from point $A$ to point $B$, moving in a semicircle of radius $1.0 \mathrm{m}$ (see figure). The magnitude of the average velocity is

A body goes from $P$ to $Q$ with a velocity of $40 \mathrm{m} {\mathrm{s}}^{-1}$ and comes back from $Q$ to $P$ with a velocity of $60 \mathrm{m} {\mathrm{s}}^{-1}$. Then, the average velocity of the body during the whole journey is _____ $\mathrm{m} {\mathrm{s}}^{-1}$.

The ratio of the numerical values of the average velocity and average speed of a body is always unity or more.

If $v=\left(2t+1\right) \mathrm{m} {\sec }^{-1}$ then average velocity from $t=0$ to $t=2 \sec$ is :-

The graph below gives the coordinate of a particle travelling along the X-axis as a function of time. $AM$ is the tangent to the curve at the starting moment and $BN$ is tangent at the end moment $\left({\theta }_1={\theta }_2=120°\right)$.

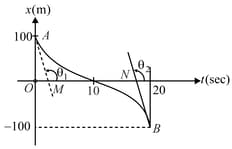
The average velocity during the first $20$ seconds is:

A scooter going due east at $10 \mathrm{m} {\mathrm{s}}^{-1}$  turns right through an angle of $90°$. What is the change in velocity of scooter on taking turn, if its speed remains constant?

Assertion: An object is at rest momentarily when it reverses the direction of its motion.

Reason: An object cannot have acceleration if the velocity of object is zero at a given instant of time

A particle moves rectilinearly possessing a parabolic $s-t$ graph. Find the average velocity of the particle over a time interval from $t=\frac{1}{2} \mathrm{s}$ to $t=1.5 \mathrm{s}$.

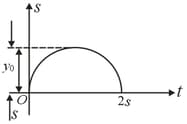
The motion of a particle is described by $\mathrm{x}={\mathrm{x}}_0(1-{\mathrm{e}}^{-\mathrm{kt}}) ; \mathrm{t}\ge 0,\mathrm{k}>0$. Find the initial velocity of the particle.

The motion of a particle is described by the equation $\mathrm{x}=\mathrm{a}\mathrm{t}+\mathrm{b}{\mathrm{t}}^2$ , where $\mathrm{a}=15\mathrm{ }\mathrm{c}\mathrm{m}\mathrm{ }{\mathrm{s}}^{-1}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\mathrm{b}=3\mathrm{ }\mathrm{c}\mathrm{m}\mathrm{ }{\mathrm{s}}^{-2}$ . It's instantaneous velocity at $\mathrm{t}=3 \mathrm{s}$  is:

The position of an object moving along $x-$axis is given by $x=a+b{t}^2$, where $a=8.5 \mathrm{m} \text{and} b=2.5\mathrm{ }\mathrm{m}\mathrm{ }{\mathrm{s}}^{-2}$ and $t$ is measured in seconds. The instantaneous velocity of the object at $t=2 \mathrm{s}$ is

The position of an object moving along x-axis is given by $\mathrm{x}=\mathrm{a}+\mathrm{b}{\mathrm{t}}^2$ , Where $\mathrm{a}=8.5\mathrm{ }\mathrm{m}$ and $\mathrm{b}=2.5\mathrm{ }\mathrm{m}\mathrm{ }{\mathrm{s}}^{-2}$ and $\mathrm{t}$ is measured in seconds. The average velocity of the object between $\mathrm{t}=2\mathrm{ }\mathrm{s}\mathrm{ }$and $\mathrm{t}=4 \mathrm{s}$ is:

Which of the following statements are incorrect ?
$\left(\mathrm{i}\right)$ Average velocity is path length divided by time interval.
$\left(\mathrm{i}\mathrm{i}\right)$ In general, speed is greater than the magnitude of the velocity.
$\left(\mathrm{i}\mathrm{i}\mathrm{i}\right)$ A particle moving in given direction with a non-zero velocity can have zero speed.
$\left(\mathrm{i}\mathrm{v}\right)$ The magnitude of average velocity is the average speed.

Velocity is given by $v=4t\left(1-2t\right),$ then find time at which velocity is maximum

A particle moves along positive branch of the curve $y=\frac{x}{2}$ where $x=\frac{t^3}{3}\text{,} x$ and $y$ are measured in metres and $t$ in seconds, then

A person walks along a straight road from his house to a market $2.5 \mathrm{km}$ away with a speed of $5 \mathrm{km} {\mathrm{h}}^{-1}$ and instantly turns back and reaches his house with a speed of $7.5 \mathrm{km} {\mathrm{h}}^{-1}.$ The average speed of the person during the time interval $0$ to $50 \min$ is (in $\mathrm{m} {\mathrm{s}}^{-1}$ )