Relative Velocity

A boat which has a speed of $5 \mathrm{km} {\mathrm{h}}^{-1}$ in still water crosses a river of width $1 \mathrm{km}$ along the shortest possible path in $15$ minutes. The velocity of the river water (in $\mathrm{km} {\mathrm{h}}^{-1}$) is

A person swims in a river aiming to reach exactly opposite point on the bank of a river. His speed of swimming is $0.5\hspace{0.17em}\mathrm{m}\mathrm{\hspace{0.17em}}{\mathrm{s}}^{-1}$ at an angle $120°$ with the direction of flow of water. The speed of water in stream is:

A bus is moving with a speed of  $10m{s}^{-1}$  on a straight road . A scooterist wishes to overtake the bus in 100 s. If the bus is at a distance of 1 km from the scooterist, with what speed should the scooterist chase the bus?

A train of 150 meters long is going towards north direction at a speed of $10\frac{m}{s}$ . A parrot flies at the speed of $5\frac{m}{s}$ towards south direction parallel to the railway track. The time taken by the parrot to cross the train is

On a frictionless horizontal surface, assumed to be the $x – y$ plane, a small trolley $A$ is moving along a straight line parallel to the $y$– axis (see figure) with a constant velocity of  $\left(\sqrt{3}-1\right)m{s}^{-1}$ . At a particular instant, when the line $OA$ makes an angle of  $45°$  with the $x$-axis, a ball is thrown along the surface from the origin $O$. Its velocity makes an angle $\varphi$ with the $x$-axis and it hits the trolley.​
The motion of the ball is observed from the frame of the trolley and the velocity vector of the ball makes an angle $\varphi$ with the x-axis in this frame.


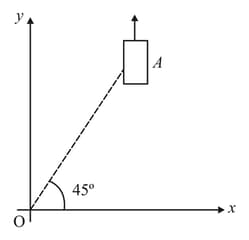
Find the speed of the ball with respect to the surface if  $\varphi =\frac{4\theta }{3}.$

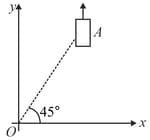
On a frictionless horizontal surface, assumed to be the x-y plane, a small trolley A is moving along a straight line parallel to the y-axis (see figure) with a constant velocity of $\left(\sqrt{3}-1\right)m{s}^{-1}$. At a particular instant, when the line OA makes an angle of $45°$ with the x-axis, a ball is thrown along the surface from the origin O. Its velocity makes an angle $\varphi$ with the x-axis and it hits the trolley. The motion of the ball is observed from the frame of trolley. Calculate the angle $\theta$ made by the velocity vector of the ball with the x-axis in this frame.

A ball is thrown from a point with a speed $v_0$  at an angle of projection $\theta$ . from the same point and at the same instant, a person starts running with a constant speed  $\frac{v_0}{2}$ to catch the ball. will the person be able to catch the ball? If yes, what should be the angle of projection?

A river is flowing from west to east at a speed of $5 \mathrm{m}$ per minute. A man on the south bank of the river, capable of swimming at $10 \mathrm{m}$ per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction

Four persons $K$, $L$, $M$, $N$ are initially at the four corners of a square of side $d$. Each person now moves with a uniform speed  $v$ in such a way that $K$ always moves directly towards $L$, L directly towards $M$, $M$ directly towards $N$, and $N$ directly towards $K$. The four persons will meet at a time

A swimmer crosses a river with minimum possible time $10$ second. And when he reaches the other end he starts swimming in the direction towards the point from where he started swimming. Keeping the direction fixed the swimmer crosses the river in $15 \sec$. The ratio of speed of swimmer with respect to water and the speed of river flow is (Assume constant speed of river & swimmer):

A motorboat is racing towards north at a speed of $10 \mathrm{m} {\mathrm{s}}^{-1}$, wind starts to blow with a speed of $10 \mathrm{m} {\mathrm{s}}^{-1}$ at $60°$ east of north. The resultant velocity of boat is 

A swimmer at one bank wants to reach directly at point $B\text{'}$ as shown in figure. If river flow speed is $5 \mathrm{m} {\mathrm{s}}^{-1}$, width of river is $4 \mathrm{m}$ and $BB\text{'}$= $3 \mathrm{m}$, then find minimum possible speed of swimmer with respect to river so that swimmer directly reaches to the point $B\text{'}$.

A passenger sitting in a train A moving at $90 \mathrm{km} {\mathrm{h}}^{-1}$ observes another train B moving in the opposite direction for $8 \mathrm{s}$. If the velocity of the train B is $54 \mathrm{km} {\mathrm{h}}^{-1}$, then length of train B is:

Two trains $A$ and $B$ of length $l$ and $4l$ are travelling into a tunnel of length $L$ in parallel tracks from opposite directions with velocities $108 \mathrm{km} {\mathrm{h}}^{-1}$ and $72 \mathrm{km} {\mathrm{h}}^{-1},$ respectively. If train $A$ take $35 \mathrm{s}$ less time than train $B$ to cross the tunnel then, length $L$ of tunnel is:

(Given $L=60 l$)

Two identical trains cross each other moving on parallel tracks, opposite in direction. Speed of one of the train is $70 \mathrm{km} {\mathrm{h}}^{-1}$ and second train has a speed of $110 \mathrm{km} {\mathrm{h}}^{-1}$. If it takes $8 \mathrm{s}$ for two trains to cross each other, then length of trains is equal to

A man is travelling at$15 \mathrm{km} {\mathrm{h}}^{-1}$ in an open truck on rainy day. He holds an umbrella at an angle$37°$ to the vertical to protect himself from the rain which is falling vertically downwards. What is the velocity of the rain?

 An aeroplane is flying with the velocity of $V_1=800 {\mathrm{kmh}}^{-1}$ relative to the air towards south. A wind with velocity of $V_2=15 \mathrm{m} {\mathrm{s}}^{-1}$ is blowing from west to east. What is the velocity of the aeroplane with respect to the earth?
 

Three particles $A, B$ and $C$ are situated at the vertices of an equilateral triangle $ABC$ of side $d$ at $t=0 .$ Each of the particles moves with constant speed $v .$ $A$ always has its velocity along $A B, B$ along $BC$ and $C$ along $CA$. At what time will the particles meet each other?

A swimmer jumps from a bridge over a canal and swims $1 \mathrm{km}$ upstream. After that first $\mathrm{km}$, he passes a floating cork. He continues swimming for half an hour and then turns around and swims back to the bridge. The swimmer and the cork reach the bridge at the same time. The swimmer has been swimming at a constant speed. How fast does the water in the canal flow?