Variable Acceleration

The displacement of a particle is represented by the following equation : $s=3t^3+7t^2+\mathrm{}\mathrm{}5t+8$ where s is in metres and t is seconds. The acceleration of the particle at $t=1 \mathrm{s}$ is

The $x-$ coordinate of a particle moving on x-axis is given by $x=3 \sin 100t+8 {\cos }^{2}50t,$ where $x$ is in $\mathrm{cm}$ and $t$ is time in seconds. Find the maximum distance the particle can move from the origin (in $\mathrm{cm}).$

A particle starts from point $A$ with zero initial velocity, moves along a straight line path with an acceleration given by $a=p-qx$ where $p, q$ are constants and $x$ is distance from point $A.$ The particle stops at point $B.$ Find the maximum velocity of the particle when $p=6$ and $q=9.$

A particle moves in a straight line with a retardation proportional to its displacement. Its loss of kinetic energy for any displacement $x$ is proportional to,

A cart is moving horizontally along a straight line with constant speed $30 \mathrm{m} {\mathrm{s}}^{-1}$. A projectile is to be fired from the moving cart in such a way that it will return to the cart after the cart has moved $80 \mathrm{m}$. At what speed (relative to the cart) must the projectile be fired (take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$)?

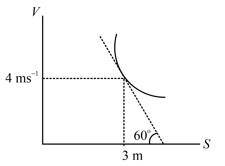
A particle is moving along a straight line whose velocity-displacement graph is as shown in the figure. What is the magnitude of acceleration when displacement is $3\mathrm{m}$?

Under the influence of a force of attraction towards the origin $O$, a particle of mass $m$ moves. The force is given by expression $\overrightarrow{F}= -\frac{k}{x^{\mathit{2}}}\stackrel{\wedge }{\mathrm{i}}$. If the particle starts from rest at $x=a$, find the speed it will attain to reach when it is at a distance $x$ from the origin.

The magnitude of displacement vector of a particle moving in a circle of radius $a$ with constant angular velocity ω as a function of time is

A particle starts from point A and moves along a straight line path with an acceleration given by a = p – qx where p, q are constants and x is distance from point A. The particle stops at point B. The maximum velocity of the particle is

The velocity of a particle $\overrightarrow{v}$ at any instant is $\mathrm{ }\overrightarrow{v}=y\widehat{i}+x\widehat{j}$ . The equation of trajectory of the particle is:

If the velocity of a particle is $\mathrm{\upsilon }=\mathrm{A}\mathrm{t}+\mathrm{B}{\mathrm{t}}^2$, where $\text{A}$ and $\text{B}$ are constants, then the distance travelled by it between $\text{1}\text{s}$ and $\text{2}\text{s}$ is:

The position (x) of a particle varies with time as $\mathrm{t}=\mathrm{\alpha }{\mathrm{x}}^2+\mathrm{\beta }\mathrm{x}$, then acceleration of particle is

A point moves with uniform acceleration and its initial speed and final speed are $1 \mathrm{m} {\mathrm{s}}^{-1}$ and $2 \mathrm{m} {\mathrm{s}}^{-1}$ respectively then, the space average of velocity over the distance moved is. (in $\mathrm{m} {\mathrm{s}}^{-1}$) :-

The distance $r$ from the origin of a particle moving in $x-y$ plane varies with time as $r=2t$ and the angle made by the radius vector with positive $x$-axis is $\mathrm{\theta }=4t$. Here, $t$ is in second, $r$ in metre and $\mathrm{\theta }$ in radian. The speed of the particle at $t=1 \sec$ is

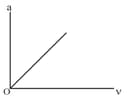
Acceleration velocity graph of a particle moving in a straight line is as shown in figure. The slope of velocity-displacement graph

A bee files a line from a point $A$ to another point $B$ in $4 \mathrm{s}$ with a velocity of $\left|t-2\right|\mathrm{m}{\mathrm{s}}^{-1}$. The distance between $A$ and $B$ in metre is

Acceleration of a body for displacement equation, $s=\frac{9t+5t^2}{3}$ is

The acceleration of a particle moving in straight line is defined by the relation $a=-4x\left(-1+\frac{1}{4}{x}^2\right)$, where $a$ is acceleration in $\mathrm{m} {\mathrm{s}}^{-2}$ and $x$ is the position in meter. If velocity $v=17 \mathrm{m} {\mathrm{s}}^{-1}$ when x = 0, then the velocity of the particle when x = 4 meter is: