Moment of Inertia and Axes Theorems

Find the moment of inertia of a uniform annular disc of mass $100 \mathrm{gm}$ having an inner radius $10 \mathrm{cm}$ and outer radius $20 \mathrm{cm}$ about an axis passing through its centre and perpendicular to its plane.

Derive an expression for the moment of inertia of an annular disc having mass $\mathrm{M}$  about an axis passing through it centre and perpendicular to it

Calculate the moment of inertia of an annular disc about an axis which lies in the plane of the disc and tangential to the outer circle. The mass of the disc is $\mathrm{M}$ and its inner radius is ${\mathrm{R}}_2$ and outer radius${\mathrm{R}}_1$ .

The moment of inertia of an annular disc of mass M, outer and inner radii R and r, about its diameter is :

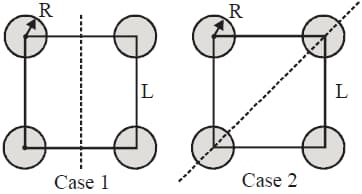
Four hollow spheres, each with a mass of $1 \mathrm{kg}$ and a radius $\mathrm{R}=10\mathrm{cm},$ are connected with massless rods to form a square with side of length $\mathrm{L}=50 \mathrm{cm},$ In case-1, the masses rotate about an axis that bisects two sides of the square. In case- 2, the masses rotate about an axis that passes through the diagonal of the square, as shown in the figure. Compute the ratio of the moments of inertia ${\mathrm{I}}_1/{\mathrm{I}}_2,$ for the two cases.

The distance in the parallel axis theorem is multiplied by _____.

The moment of inertia of a hollow cubical box of mass $M$ and side length $a$, about an axis passing through centres of two opposite faces, is equal to $\frac{xM{a}^2}{18}$. The value of $x$ is

The moment of inertia of a hollow cubical box of mass $M$ and side length $a$, about an axis passing through centres of two opposite faces, is equal to $\frac{xM{a}^2}{18}$. The value of $x$ is

A circular disc $A$ of radius $r$ is made from an iron plate of thickness $t$ and another circular disc $B$ of radius $4 r$ is made from an iron plate of thickness $\frac{t }{4}$. What is the relation between the moments of inertia of $I_{\mathrm{A}}$ and $I_{\mathrm{B}}$?

The moment of inertia of a thin rod of length $L$ and mass $M$ about an axis passing through a point at a distance $\frac{L}{3}$ from one of its ends and perpendicular to the rod is,

A thin wire of length $L$ and uniform linear mass density $\mathrm{\rho }$ is bent into a circular loop with centre $O$ as shown. The moment of inertia of the loop about the axis $XX\text{'}$ will be,

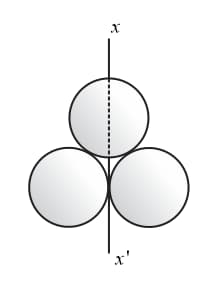
Three solid spheres of mass $M$ and radius $R$ are shown in the figure. The moment of inertia of the system about $xx\text{'}$ axis will be,

The moment of inertia of a circular ring about an axis passing through its centre and perpendicular to its plane is $200 \mathrm{g} {\mathrm{cm}}^2$. If the radius of the ring is $5 \mathrm{cm}$, find the mass of the ring.

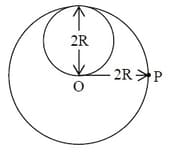
A lamina is made by removing a small disc of diameter $2\mathrm{R}$ from a bigger disc of uniform mass density and radius $2\mathrm{R}$, as shown in the figure. The moment of inertia of this lamina about axes perpendicular to the plane of the lamina and passing through the points $\mathrm{O}$ and $\mathrm{P}$ is ${\mathrm{I}}_{\mathrm{O}}$ and ${\mathrm{I}}_{\mathrm{P}}$​ respectively. If the ratio $\frac{{\mathrm{I}}_{\mathrm{P}}}{{\mathrm{I}}_{\mathrm{O}}}=\frac{\mathrm{m}}{\mathrm{n}}$, where $\mathrm{m}$ and $\mathrm{n}$ are the smallest integers, then what is the value of $\mathrm{m}+\mathrm{n}$?

A uniform cylinder has a radius $R$ and length $L$. If the moment of inertia of this cylinder about an axis passing through its centre and normal to its circular face is equal to the moment of inertia of the same cylinder about an axis passing through its centre and perpendicular to its length, then

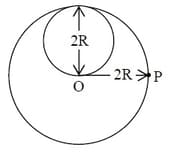
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure.The moment of inertia of this lamina about axes passing though O and P is I_O and I_P​ respectively. Both of these axes are perpendicular to the plane of the lamina.The ratio I_P / I_O to the nearest integer is 

The moment of inertia of a solid sphere of mass $M$ and radius $R$ about a tangent to the sphere is _____$M{R}^2$(Write the answer upto one decimal place).

State and prove principle of perpendicular axes.

State and prove principle of parallel axes.

A thin uniform rod of length $1$ m and mass $1$ kg is rotating about an axis passing through its centre and perpendicular to its length. Calculate the moment of inertia and radius of gyration of the rod about an axis passing through a point midway between the centre and its edge, perpendicular to its length.