Kinetic Energy due to Rotation

A couple produces

The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is

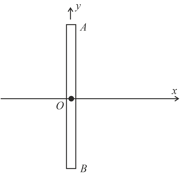
At shown instant a thin uniform rod $\mathrm{AB}$ of length $L=1 \mathrm{m}$ and mass $m=1 \mathrm{kg}$ is coincident with $y-$axis such that centre of rod is at origin. The velocity of end $A$ and centre $O$ of rod at shown instant are ${\overrightarrow{v}}_{\mathrm{A}}=-2\hat{\mathrm{i}} \mathrm{m} {\mathrm{s}}^{-1}$ and ${\overrightarrow{v}}_0=10\hat{\mathrm{i}} \mathrm{m} {\mathrm{s}}^{-1}$ respectively. Then the kinetic energy of rod at the shown instant is:

A uniform circular disc of mass $400 \mathrm{g}$ and radius $4.0 \mathrm{cm}$ is rotated about one of its diameter at an angular speed of $10 \mathrm{rad} {\mathrm{s}}^{-1}$. The kinetic energy of the disc is

The ring of radius $1 \mathrm{m}$ and mass $15 \mathrm{kg}$ is rotating about its diameter with angular velocity of $25\mathrm{rad}/\sec$. Its kinetic energy is

A couple produces,

The angular momentum of a particle describing uniform circular motion is $L$. If its kinetic energy is halved and angular velocity doubled, its new angular momentum is

A body having a moment of inertia about its axis of rotation equal to $3 \mathrm{kg} {\mathrm{m}}^2$ is rotating with an angular velocity of $3 \mathrm{rad} {\mathrm{s}}^{-1}$. Kinetic energy of this rotating body is same as that of a body of mass $27 \mathrm{kg}$ moving with a velocity $v$. The value of $v$ is

The rotational $KE$ of a body is $E$ and its moment of inertia is $I$. The angular momentum is

Energy of $1000 \mathrm{J}$ is spent to increase the angular speed of a wheel from $20 \mathrm{rad} {\mathrm{s}}^{-1}$ to $30 \mathrm{rad} {\mathrm{s}}^{-1}$. Moment of inertia of the wheel in $\mathrm{kg} {\mathrm{m}}^2$ 

A wheel of mass $10 \mathrm{kg}$ and radius $0.8 \mathrm{m}$ is rolling on a road with an angular speed $20{\mathrm{rads}}^{-1}$ without sliding. The moment of inertia of the wheel about the axis of rotation is $1.2{\mathrm{kgm}}^2,$ then the percentage of rotational kinetic energy in the total kinetic energy of the wheel is ____________(approximately)

A wheel is at rest in horizontal position. Its $M\mathit{.}I\mathit{.}$ about vertical axis passing through its centre is $\text{'}I\text{'}$. A constant torque '$\tau$' acts on it for $\text{'}t\text{'}$ second. The change in rotational kinetic energy is

A uniform sphere of mass $\mathrm{m}=2.5 \mathrm{kg}$ and radius $R=10 \mathrm{cm}$ rotates with an angular velocity, $\omega =200 \mathrm{rad} {\mathrm{s}}^{-1}$ about its diameter. Find its kinetic energy.

Kinetic energy of rotation of a flywheel of radius $2 \mathrm{m},$ mass $8 \mathrm{kg}$ and angular speed $4 \mathrm{rad} {\mathrm{s}}^{-1}$ about an axis perpendicular to its plane and passing through its center is

If the rotational kinetic energy of a body is increased by $300 \%$ then the percentage increase in its angular momentum :-

A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque $\tau$ on the ring, it stops after making $n$ revolutions. After how many revolutions will the disc stop, if the retarding torque on it is also $\tau$?

A disc is rolling on an inclined plane. What fraction of its total energy will be as rotational energy?

Energy of $1000 \mathrm{J}$ is spent to increase the angular speed of a wheel from $20 \mathrm{rad}/\mathrm{s}$ to $30 \mathrm{rad}/\mathrm{s}$. Moment of inertia of the wheel in $\mathrm{kg} {\mathrm{m}}^2$ 

Two metallic spheres of equal outer radii are found to have same moment of inertia about their respective diameters. Then, which of the following statement(s) is/are true?

A uniform sphere of mass $\mathrm{m}=2.5 \mathrm{kg}$ and radius $R=10 \mathrm{cm}$ rotates with an angular velocity, $\omega =200 \mathrm{rad} {\mathrm{s}}^{-1}$ about its diameter. Find its kinetic energy.