Pure Rolling

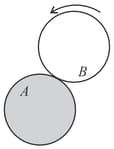
A flat surface of a thin uniform disk $A$ of radius $R$ is glued to a horizontal table. Another thin uniform disk $B$ of mass $M$ and with the same radius $R$ rolls without slipping on the circumference of $A$, as shown in the figure. A flat surface of $B$ also lies on the plane of the table. The center of mass of $B$ has fixed angular speed $\omega$ about the vertical axis passing through the center of $A$. The angular momentum of $B$ is $nM\omega R^2$ with respect to the center of $A$. Which of the following is the value of $n$?

​​​​​​​

These questions consists of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: A solid sphere cannot roll without slipping on smooth horizontal surface.

Reason: If the sphere is left free on smooth inclined surface, it cannot roll without slipping.

A uniform solid ball of mass '$m$' rolls without sliding on a fixed horizontal surface. The velocity of the lowest point of the ball with respect to the center of the ball is $v$. The total kinetic energy of the ball is:

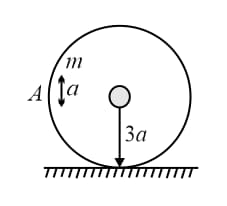
A ring of radius $3a$ is fixed rigidly on a table. A small ring whose mass is $m$ and radius $a$ rolls without slipping inside it as shown in the figure. The small ring is released from position $A$. When it reaches the lowest point, the speed of the centre of the ring at that time would be,

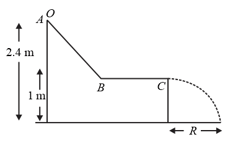
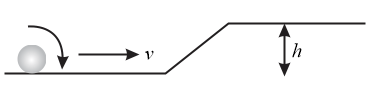
A small sphere rolls down without slipping from the top of a track in a vertical plane as shown. The track has an elevated section and a horizontal path. The horizontal part is $1.0 \mathrm{m}$ above the ground level and the top of the track is $2.4 \mathrm{m}$ above the ground. Find the distance on the ground with respect to a point $B$ where the sphere lands.

A solid sphere is rolling on a frictionless surface, as shown in figure with a translational velocity $v \mathrm{m} {\mathrm{s}}^{-1}$. If it has to climb the inclined surface, then $v$ should be

In the previous, which of the bodies reaches the ground with maximum rotational kinetic energy?

What is the work done against friction during rolling, if length of the incline is $1$ meter?

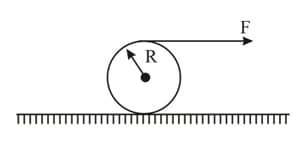
A ring of mass $m$ and radius $R$ is acted upon by a force $F$ as shown in the figure. There is sufficient friction between the ring and the ground. The force of friction necessary for pure rolling is

A small pulley of radius $20 \mathrm{cm}$ and moment of inertia $0.32 \mathrm{kg} {\mathrm{m}}^2$ is used to hang a $2 \mathrm{kg}$ mass with the help of massless string. If the block is released, for no slipping condition acceleration of the block will be

A rod of uniform mass and of length $L$ can freely rotate in a vertical plane about an axis passing through $O.$ The angular velocity of the rod when it falls from position $P$ to $P^{\text{'}}$ through an angle $\alpha$ is

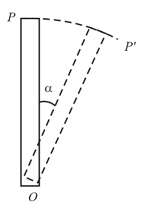
A solid sphere of mass $M$ rolls without slipping on an inclined plane of inclination $\mathrm{\theta }$. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping?

A solid cylinder and a solid sphere both having the same mass and radius are released from a rough inclined plane. Both roll without slipping. Then,

The ratio of the time taken by a solid sphere and that taken by a disc of the same mass and radius to roll down a rough inclined plane from rest from the same height is

A hollow smooth uniform sphere A of mass $\text{'}m\text{'}$ rolls without sliding on a smooth horizontal surface. It collides elastically and head on with another stationary smooth solid sphere $B$ of the same mass $m$ and same radius. The ratio of kinetic energy of $\text{'}B\text{'}$ to that of $\text{'}A\text{'}$ just after the collision is :

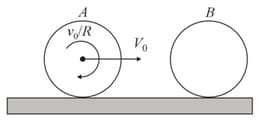
A uniform solid sphere of radius $r$ is released on a rough horizontal floor after imparting it an initial horizontal velocity vo and angular velocity ${\omega }_0$ as shown in the figure below. Coefficient of friction between sphere and ground is $\mu .$ What should be the relation between vo and $\omega 0$ so that the sphere comes to permanent rest after sometime?

A uniform solid sphere is released from the top point of an incline plane. If the incline surface is smooth the sphere takes a time $t_1$ to slide down. If the surface of incline is sufficient rough so that the sphere can roll without sliding the sphere takes time $t_2$ to roll down the same incline, $\frac{t_1}{t_2}$ will be :

In rotational motion of a rigid body, all particles move with _____.

The ratio of the accelerations for a solid sphere (mass $\text{'}m\text{'}$ and radius $\text{'}R\text{'}$) rolling down an incline of anlge $\text{'}\theta \text{'}$ without slipping and slipping down the incline without rolling is

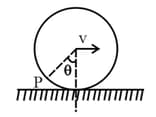
$\mathrm{A}$ hoop rolls on $\mathrm{a}$ horizontal ground without slipping with linear speed $\mathrm{v}$. Speed of $\mathrm{a}$ particle $\mathrm{P}$ on the circumference of the hoop at angle $\theta$ is :