Centre of Mass and its Motion

Find the centre of mass of a thin, uniform disc of radius $R$ from which a small concentric disc of radius $r$ is cut.

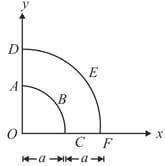
$ABCFED$ is a uniform plate (shown in figure). $ABC$ and $DEF$ are circular arcs with common centre at $O$ and having radii $a$ and $2a$ respectively. This plate is lying on a smooth horizontal table. A particle of mass half the mass of the plate strikes the plate at point $A$ while travelling horizontally along the $x$ direction with velocity $u$. The particle hits the plate and rebounds along negative $x$ with velocity $\frac{u}{2}$. Find the velocity of point $D$ of the plate immediately after the impact. [Take $\frac{28}{9\pi }\simeq 1$]

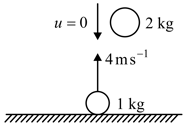
A ball of mass $1 \mathrm{kg}$ is thrown up with an initial speed of $4 \mathrm{m} {\mathrm{s}}^{-1}$. A second ball of mass $2 \mathrm{kg}$ is released from rest from some height as shown in the figure. For the motion of both balls in air :

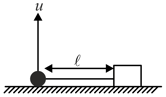
A small ball is connected to a block by a light string of length $\ell$. Both are initially on the ground. There is sufficient friction on the ground to prevent the block from slipping. The ball is projected vertically up with a velocity $u$, where $2 g\ell <{\mathrm{u}}^2<3 g\ell$. The centre of mass of the block $+$ ball system is $C$

A proton and an ${}_{\alpha }$ - particle are projected with same speed $V_0=\sqrt{\frac{K{e}^2}{mL}}$ towards each other from very large distance and the perpendicular distance between their initial line of motions is '$L$' as shown in fig. Mass of proton '$m$' and it's charge '$e$' and Mass of the $\alpha$ - particle is taken as $4 \mathrm{m}$ and it's charge $2e$ [neglect gravitation effects and magnetic effects $\left[K=\frac{1}{4\pi {\epsilon }_0}\right]$

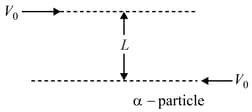
The closest approach distance between them is $r_1\times L$. Find $r_1$

A rigid rod of mass $6 \mathrm{m}$ and length $2$ meters is lying at rest on a smooth horizontal table as shown in the figure .Two point masses of equal mass $5 \mathrm{m}$ collide and stick to the rod at the same instant. Before collision they were both moving with a speed of $4 \mathrm{m} {\mathrm{s}}^{-1}$.

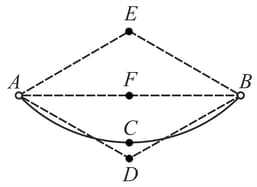
A uniform rope suspended between two level nails $A$ and $B$ assume a curved shape $ABC$ as shown in the figure. The midpoint $C$ of the rope is pulled vertically down to a position $D$ to make a $V$ shape and released. When the rope again acquires the curved shape $ACB$, the midpoint is pulled vertically upto a position $E$ to make an inverted $V$ shape. If in these two pulling processes, total work done by the pulling agency is $10 \mathrm{J}$ . How much work will be done by the pulling agency in lifting vertically the midpoint from equilibrium to a position $F$ in level with the nails ?(in $\mathrm{J}$)

A double star is a system of two stars rotating about their centre of mass only under their mutual gravitational attraction. Let the stars have masses $m$ and $2 \mathrm{m}$and let their separation be $l$. Their time period of rotation about their centre of mass will be proportional to

At an instant, the point $P$ in the figre represents the instantaneous centre of rotation for a uniform rectangular plate $ABCD\left(12\mathrm{cm}\times 10\mathrm{cm}\right)$. At the given instant the point $A$ (corner) has velocity $24\frac{\mathrm{cm}}{\sec }\left(-\hat{j}\right)$. The magnitude of the velocity of the centre of mass of the plate is

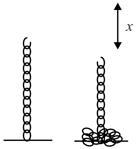
A chain of mass $m$ and length $L$ is initially held in vertical position as shown in the figure. It is released from rest, then which of the following graph(s) is/are correct. Here $N$ represents normal force by the ground on the chain and $v$ represents velocity of free end

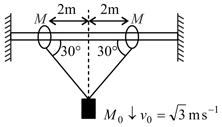
Two rings, each of mass $M=100\mathrm{gm}$ are constrained to move along a fixed horizontal rod. An ideal string is connected with rings and a block of mass $M_0=200\mathrm{gm}$ is connected to the mid point of string. At a certain moment the mass $m$ is moving downward with velocity $\sqrt{3}$ ${\mathrm{ms}}^{-1}$. Find the speed of ring of $M$ at the moment.

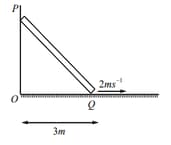
A ladder $PQ$ of length $5\mathrm{m}$ inclined to a vertical wall is slipping over a horizontal surface with a velocity of $2{ \mathrm{ms}}^{-1}$, When $\mathrm{Q}$ is at a distance $3\mathrm{m}$ from the ground. Calculate the velocity of centre of mass the rod at this moment

A uniform thin hollow hemi-spherical shell of mass $m=1\mathrm{kg}$ and radius $R=0.25\mathrm{m}$ is released form rest with its diametrical plane vertical on a very rough horizontal surface as shown

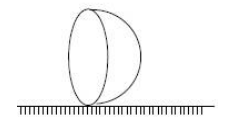
It does not slip on the floor during its subsequent motion. Calculate Normal force exerted on it by floor, (in $N$). When its kinetic energy is maximum (take $g=9.80 {\mathrm{ms}}^{-2}$)

A body is launched from the earth's surface at an angle $\alpha =30°$ to the horizontal at a speed $v_0=\sqrt{\frac{1.5\mathrm{GM}}{R}}$. Neglecting air resistance and earth's rotation, if the maximum height to which the body will rise is $x\times R$ then find $x$

A proton and an $\alpha$-particle are projected with same speed $V_0=\sqrt{\frac{K{e}^2}{mL}}$ towards each other from very large distance and the perpendicular distance between their initial line of motions is '$L$' as shown in fig. Mass of proton '$m$' and it's charge '$e$' and Mass of the $\alpha -$particle is taken as $4\mathrm{m}$ and it's charge $2\mathrm{e}$ [neglect gravitation effects and magnetic effects $\left[K=\frac{1}{4\pi {\epsilon }_0}\right]$

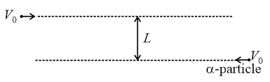
The closest approach distance between them is $r_1\times L$. Find $r_1$

A star is modelled as a uniform spherical distribution of matter. Keeping mass of the star constant, how gravitational pressure '$P$' at centre of star depends on volume '$V$' of the star ?

A uniform solid cylinder of radius $R=15 \mathrm{cm}$ rolls over a horizontal plane passing in to an inclined plane forming an angle $\alpha =30°$ with the horizontal. Find the maximum value of the velocity $v_0$ which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.

Imagine a hole drilled along the radius of earth. A uniform rod of length equal to radius $R$ of earth is inserted into the hole. The distance of centre of gravity of the rod from the centre of earth is $\frac{n}{3}R$, find the value of $n$.

A homogeneous rod leaves on a frictionless horizontal plane making the angle $\alpha =60°$. If released from rest it will fall and its end which is in contact with the plane at the beginning will move along the plane until the other end reaches the plane. The ratio of the length of the rod to the distance covered by the end on the plane at the beginning is ___________