Rolling Motion
Rolling Motion: Overview
This topic consists of various concepts like Rolling Motion of a Rigid Body,Pure and Impure Rolling Motion,Velocity of Points in Rolling, etc.
Important Questions on Rolling Motion
A uniform disc of mass and radius is projected with velocity at on a rough horizontal surface. It starts off with a purely sliding motion at. After it acquires a purely rolling motion (see figure). The total kinetic energy of the disc after will be-------- J (given, coefficient of friction is and ).
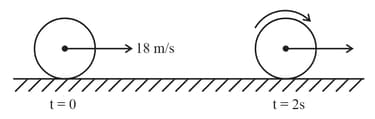
A hollow sphere is rolling (without slipping) on horizontal surface with velocity . It then moves up a curved track. If sliding does not occur, then the maximum height moved-up by sphere is
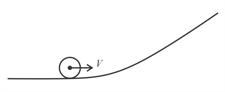
In case of pure rolling, what will be the velocity of point A of the ring of radius ?
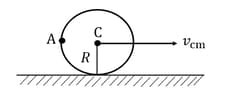
A uniform solid sphere is given velocity and angular velocity and placed on a rough horizontal surface as shown. The velocity of centre of mass when pure rolling starts, is
A wheel is rolling along the ground with a speed of . The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is equal to
A flat surface of a thin uniform disk of radius is glued to a horizontal table. Another thin uniform disk of mass and with the same radius rolls without slipping on the circumference of , as shown in the figure. A flat surface of also lies on the plane of the table. The center of mass of has fixed angular speed about the vertical axis passing through the center of . The angular momentum of is with respect to the center of . Which of the following is the value of ?
At time , a disk of radius starts to roll without slipping on a horizontal plane with an angular acceleration of . A small stone is stuck to the disk. At , it is at the contact point of the disk and the plane. Later, at time , the stone detaches itself and flies off tangentially from the disk. The maximum height (in ) reached by the stone measured from the plane is . The value of is [Take .]
If the numerical value has more than two decimal places, truncate/round-off the value to TWO decimal places.
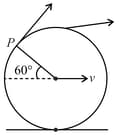
A disc of radius is rolling on a rough horizontal surface. Velocity of centre of mass is . The magnitude of velocity of the point (as shown in the figure) on the periphery of disc is
A uniform disc of mass 2 kg and radius 3 cm is rolling down on a rough inclined plane of inclination 0 = 37°. The acceleration of its centre is (g = 10 m/s²)
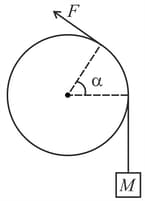
A mass hangs from a light rope which passes over a rough cylinder, the coefficient of friction being and the angle of lap being . The least value of , the tension in the upper part of the rope required to prevent the mass from falling is . The value of is:
A cylinder is rolling without slipping on an inclined plane. Show that to prevent slipping the condition
Two identical rods one and two each of mass and length are performing general plane motion on the horizontal plane as shown in the figure. If is velocity of centre of mass of both the rods and is the angular speed about the vertical axis, then angular momentum of rod in the frame of reference of centre of mass of rod at the given instant will be
A semi-Cylindrical wedge of mass and radius is placed on a horizontal smooth surface. A solid cylinder of mass and radius is placed at the top of the wedge as shown in the figure, and released with a gentle rightward push. There is no friction between the curved surface of semi cylinder and solid cylinder. Find the velocity of the wedge when the line makes an angle of with the vertical. (given and )
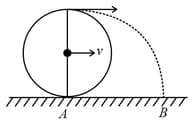
A wheel of radius rolls without slipping with a speed over a horizontal road. When it is at a point on the road; a small lump of mud separates from the wheel at its highest point and lands on the road at a point . Then
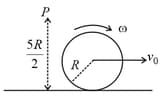
The minimum force required to roll a rigid sphere up a vertical wall is (The coefficient of friction between sphere and the wall is )
A disc of mass and radius rolls without slipping on a horizontal surface (see figure).
If the speed of its centre is , then the magnitude of the angular momentum of the disc about a fixed point at a height above the horizontal surface
A ring and a disc have the same mass and roll without slipping with the same linear velocity . If the total of the ring is , the of the disc must be
If a thin ring is subjected to a force as shown in the figure. Find the force of friction required to make sure that the ring does pure rolling on the rough surface.
These questions consists of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.
Assertion: A solid sphere cannot roll without slipping on smooth horizontal surface.
Reason: If the sphere is left free on smooth inclined surface, it cannot roll without slipping.
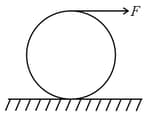
A uniform solid cylindrical roller of mass is being pulled on horizontal surface with force parallel to the surface applied at its centre. If the acceleration of the cylinder is and it is rolling without slipping, then the value of is
