Surface Tension

The maximum area of tension reinforcement in beams shall not exceed:

Water rises to a height of $10 \mathrm{cm}$ in a capillary tube and mercury falls to a depth of $3.5 \mathrm{cm}$ in the same capillary tube. If the density of mercury is $13.6 \mathrm{gm} {\mathrm{cc}}^{-1}$ and its angle of contact is $135°$ and density of water is $1 \mathrm{gm} {\mathrm{cc}}^{-1}$ and its angle of contact is $0°$, then the ratio of surface tensions of the two liquids is $(\cos 135°=0.7)$

The radii of two soap bubbles are $r_1$ and $r_2$ . In isothermal conditions, two meet together in vacuum. Then the radius of the resultant bubble is given by

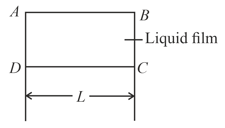
A film of water is formed between two straight parallel wires of length $10 \mathrm{cm}$ each separated by $0.5 \mathrm{cm}$. if their separation is increased by $1 \mathrm{mm}$ while still maintaining their parallelism, how much work will have to be done (surface tension of water $= 7.2\times {10}^{-2} \mathrm{N} {\mathrm{m}}^{-1}$)

Radius of a soap bubble is increased from $R$ to $2R$  work done in this process in terms of surface tension is

Radius of a soap bubble is increased from $R$ to $2R$ work done in this process in terms of surface tension is

A liquid film is formed over a frame $ABCD$ as shown in figure. Wire $CD$ can slide without friction. The mass to be hung from $CD$ to keep it in equilibrium is

There is horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius $R$. If the surface tension of the loop be $T$ , then what will be the tension in the thread​

A $10 \mathrm{cm}$ long wire is placed horizontally on the surface of water and is gently pulled up with a force of  $2\times {\mathrm{10}}^{-2} \mathrm{N}$ to keep the wire in equilibrium. The surface tension in  $\mathrm{N} {\mathrm{m}}^{-1}$ of water is

A thin metal disc of radius $r$ floats on water surface and bends the surface downwards along the perimeter making an angle $\theta$ with vertical edge of disc. If the disc displaces a weight of water $W$ and surface tension of water is $T$ , then the weight of metal disc is​

A wooden stick $2 \mathrm{m}$ long is floating on the surface of water. The surface tension of water $0.07 \mathrm{N} {\mathrm{m}}^{-1}$. By putting soap solution on one side of the stick, the surface tension is reduced to $0.06 \mathrm{N} {\mathrm{m}}^{-1}$. The net force on the stick will be

Floating a needle on the surface of the _____ is an example of surface tension.

Explain some examples which illustrate the existence of surface tension.

Adding soap _____ the water's surface tension so the drop becomes weaker and breaks apart sooner. 

Small insects such as the water strider can walk on water because their weight is not enough to penetrate the surface.

What are the examples illustrating the effects of surface tension?

The following observations were taken for determining surface tension T of water by capillary method:

diameter of capillary, $D=1.25\times {10}^{-2}m$

rise of water, $h=1.45\times {10}^{-2}m.$

Using $g=9.80 m/s^2$ and the simplified relation $T=\frac{rhg}{2}\times {10}^{3}N/m,$ the possible error in surface tension is closest to:

A soap bubble having radius of $1 \mathrm{m}\mathrm{m}$ is blown from a detergent solution having a surface tension of $2.5\times {10}^{-2}\mathrm{N} {\mathrm{m}}^{-1}.$ The pressure inside the bubble equals at a point $Z_0$ below the free surface of water in a container. Taking $g=10 \mathrm{m} {\mathrm{s}}^{-2},$ density of water $={10}^3 \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3},$ the value of $Z_0$ is

A small spherical droplet of density $d$ is floating exactly half immersed in a liquid of density $\rho$ and surface tension $T.$ The radius of the droplet is (take note that the surface tension applies an upward force on the droplet):

When water is filled carefully in a glass, one can fill it to a height $h$ above the rim of the glass due to the surface tension of water. To calculate $h$ just before water starts flowing, model the shape of the water above the rim as a disc of thickness $h$ having semicircular edges, as shown schematically in the figure. When the pressure of water at the bottom of this disc exceeds what can be withstood due to the surface tension, the water surface breaks near the rim and water starts flowing from there. If the density of water, its surface tension and the acceleration due to gravity are ${10}^3 \mathrm{kg}{ \mathrm{m}}^{-3}, 0.07 \mathrm{N} {\mathrm{m}}^{-1}$ and $10{ \mathrm{m} \mathrm{s}}^{-2},$ respectively, the value of $\left[h\right]$ (in $\mathrm{mm}$) is_______, where $\left[ \right]$ is the greatest integer function..