Conservation of Mechanical Energy

A small sphere is attached to a cord and rotates in a vertical circle about a point $O$. If the range speed of the sphere is increased, the cord is most likely to break at the orientation when the mass is at:

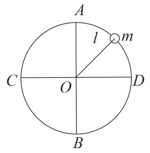
A stone tied to a string is rotated in a vertical circle. The minimum speed of the stone during a complete vertical circular motion 

A smooth semicircular wire track of radius $R$ is fixed in a vertical plane One end of a massless spring of natural length  $\frac{\mathrm{}\mathrm{}\mathrm{}3R}{4}$  is attached to the lowest point $O$of the wire track. A small ring of mass $m$ which can slide on the track is attached to the other end of the spring. The ring is held stationary at point $P$ such that the spring makes an angle of  $60°$ with the vertical. The spring constant $K=\frac{mg}{R}$ . Consider the instant when the ring is released. Find the normal reaction on the ring by the track.

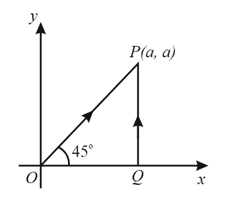
A particle is moved from $\left(0, 0\right)$ to $\left(a, a\right)$ under a force $F=(3\hat{\mathrm{i}}+4\hat{\mathrm{j}})$ from two paths. Path $1$ is $OP$ and path $2$ is $OQP$. Let $W_1$ and $W_2$ be the work done by this force in these two paths. Then,

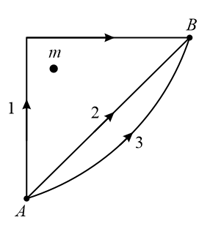
If $W_1, W_2$ and $W_3$ represent the work done in moving a particle from $A$ to $B$ along three different paths $1, 2$ and $3$, respectively (as shown), in the gravitational field of a point mass $m$, find the correct relation between $W_1, W_2$ and $W_3$.

A pendulum string of length $𝓁$ moves up to a horizontal position as shown in figure and released.




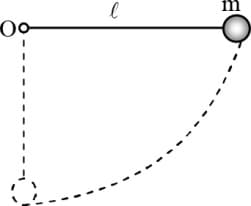
What should be the minimum strength of the string to withstand the tension as the pendulum passes through the position of equilibrium? The mass of the pendulum is $m$.

A particle is tied to a string describes a vertical circular motion of radius $r$ continually. If it has a velocity $\sqrt{3gr}$ at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

The velocity of a body, undergoing motion in a vertical circle is maximum at _____ .
(Choose from: top/bottom)

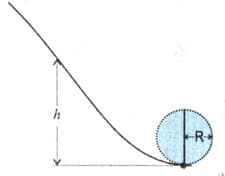
A ball is released from height along the slope and move along a circular track of radius $R$ without falling vertically downwards. Show that $h=\frac{5}{2}R$.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg}$ wt, calculate maximum number of revolutions it can complete in a minute.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg} \mathrm{wt}$, calculate speed of object.

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at highest position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at mid position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at lowest position. 
 

Obtain expressions for tension at highest position, midway position and bottom position for an object revolving in a vertical circle.

Derive an expression for difference in tensions at highest and lowest point for a particle performing vertical circular motion.

A particle is attached at one end of a string of length $l$ whose other end is fixed. It is moving in a circular path in the vertical plane such that at any position. The tension in the string is $T$ and the acceleration of the particle is $a$. The velocity of the particle at the lowest point is $u$. Then find the condition at which $\overrightarrow{T}·\overrightarrow{a}$ will be positive at the lowest point.

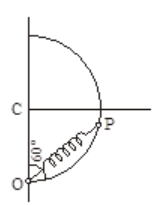
A particle is projected horizontally from the top of a smooth sphere of the radius $a$ with a velocity $u$ so that it slides down the outside of the sphere. After falling through a height of $\frac{a}{4}$, the particle leaves the sphere. Find the value of $u$.

A bob of mass $m$ of a simple pendulum of length $l$ displaced from position $O$ to $P$. $P$ is $h$ height above the position $O$. Then it is released from the position $P$. The velocity of the bob is $v$ at $O$. Find the tension in the string when the bob passes through the equilibrium position $O$ (neglect friction).