Vertical Circular Motion

A small sphere is attached to a cord and rotates in a vertical circle about a point $O$. If the range speed of the sphere is increased, the cord is most likely to break at the orientation when the mass is at:

A stone tied to a string is rotated in a vertical circle. The minimum speed of the stone during a complete vertical circular motion 

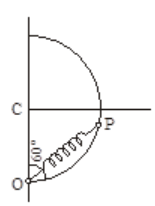
A smooth semicircular wire track of radius $R$ is fixed in a vertical plane One end of a massless spring of natural length  $\frac{\mathrm{}\mathrm{}\mathrm{}3R}{4}$  is attached to the lowest point $O$of the wire track. A small ring of mass $m$ which can slide on the track is attached to the other end of the spring. The ring is held stationary at point $P$ such that the spring makes an angle of  $60°$ with the vertical. The spring constant $K=\frac{mg}{R}$ . Consider the instant when the ring is released. Find the normal reaction on the ring by the track.

A point mass $\mathrm{M}$ is hanging by a string of length $\mathrm{l}.$ The velocity $v$ which must be imparted to it in order for it to just barely reach the top is

A pendulum string of length $𝓁$ moves up to a horizontal position as shown in figure and released.




What should be the minimum strength of the string to withstand the tension as the pendulum passes through the position of equilibrium? The mass of the pendulum is $m$.

 In a Circus, a motor-cyclist having mass of $50 \mathrm{kg}$ moves in a spherical cage of radius $3 \mathrm{m}$. Least velocity with which he must pass the highest point without losing contact. 

A stone tied with a string, is rotated in a vertical circle. The minimum speed with which the string has to be rotated

A particle is tied to a string describes a vertical circular motion of radius $r$ continually. If it has a velocity $\sqrt{3gr}$ at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

A bucket, full of water is revolved in a vertical circle of radius $1.5 \mathrm{m}.$ The maximum time period of revolution so that the water doesn't fall out of the bucket is $\left(g\approx {\pi }^2\right)$

A particle is attached at one end of a string of length $l$ whose other end is fixed. It is moving in a circular path in the vertical plane such that at any position. The tension in the string is $T$ and the acceleration of the particle is $a$. The velocity of the particle at the lowest point is $u$. Then find the condition at which $\overrightarrow{T}·\overrightarrow{a}$ will be positive at the lowest point.

A particle is projected horizontally from the top of a smooth sphere of the radius $a$ with a velocity $u$ so that it slides down the outside of the sphere. After falling through a height of $\frac{a}{4}$, the particle leaves the sphere. Find the value of $u$.

A bob of mass $m$ of a simple pendulum of length $l$ displaced from position $O$ to $P$. $P$ is $h$ height above the position $O$. Then it is released from the position $P$. The velocity of the bob is $v$ at $O$. Find the tension in the string when the bob passes through the equilibrium position $O$ (neglect friction).

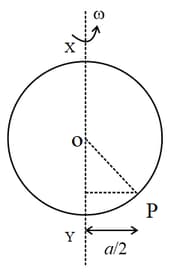
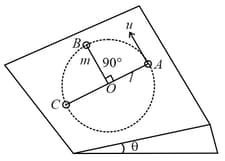
Figure shows a small ring $\mathrm{P}$ is threaded on a smooth wire bent in the form of a circle of radius $a$ and centre $\mathrm{O}$. The wire is rotating with constant angular speed $\omega$ about a vertical diameter $\mathrm{XY}$, while the ring remains at rests relative to the wire at a distance $\frac{a}{2}$ from $\mathrm{XY}$. What is the value of ${\omega }^2$ ?

A simple pendulum is made by suspending a bob with a light string. The bob is imparted a horizontal velocity such that it just completes full circular trajectory in vertical plane. What is the difference in tension between lowest and highest point of path?

 A pendulum has an angular amplitude $\theta$. Tensions in the string when the pendulum is at the extreme position and at the bottom are $T_1$ and $T_2$ respectively. If $T_2=2T_1$ , then $\theta$ is equal to :-

A particle of mass $m$ is suspended by a light, inextensible string of length $l$ from a point $O$ fixed on a smooth inclined plane of inclination $\theta$ with the horizontal. The sphere is moving in a circle on the incline as shown. If the sphere has a velocity u at the top most position A. Then,

Block $A$ is placed on the wedge $B$ at a height $h$ above the ground. Block and the two wedges are of the same mass $m$. Neglect friction everywhere.

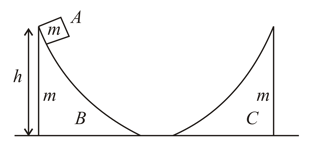
Find the velocity of $A$ when it has slid down to the ground from wedge $C$.

A uniform rod of mass $M$ and length $l$ was held in a horizontal position and one end of this rod is fixed. Now the other end of this rod is attached with a point mass $m$ and is given a speed in the vertically downward direction such that the point mass just reaches the topmost point. The initial speed given to the ball is

A uniform rod of mass $M$ and length $l$ was held in a horizontal position and one end of this rod is fixed. Now the other end of this rod is attached with a point mass $m$ and is given a speed in the vertically downward direction such that the point mass just reaches the topmost point. The change in potential energy of the system (point mass+rod) is