Mass-energy and Nuclear Binding Energy

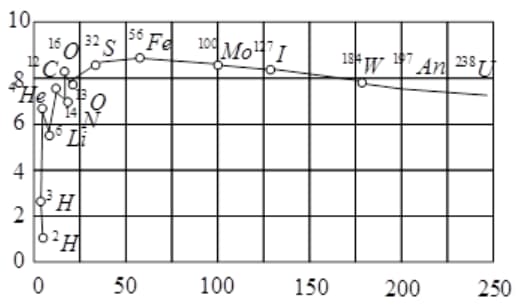
The plot of the binding energy per nucleon versus the mass number A for a large number of nuclei,  $2\le A\le 240$  is shown in Fig. In which range the binding energy per nucleon is constant?

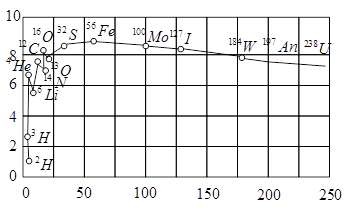
The plot of the binding energy per nucleon versus the mass number A for a large number of nuclei,  $2\le A\le 240$  is shown in Fig. In which range the binding energy per nucleon is constant?

Calculate the energy released in MeV in the following nuclear reaction :<

${}_{92}^{238}\text{U}\to {}_{90}^{234}\text{Th}+{}_2^4\text{He}+\text{Q}$

[Mass of  ${}_{92}^{238}\text{U}$ = 238.05079 u]

Mass of  ${}_{90}^{234}\text{Th}$ = 234.043630 u

Mass of  ${}_2^4\text{He}$  = 4.002600 u

1 u = 931.5 MeV

$\text{Mass of neutron}=1.008665 \mathrm{u}$

The binding energies per nucleon for deuteron (${}_1\mathrm{H}^2$) and helium (${}_2\mathrm{He}^4$) are $1.1 \mathrm{MeV}$ and $7.0 \mathrm{MeV}$ respectively. The energy released when two deuterons fuse to form a helium nucleus (${}_2\mathrm{He}^4$) is

In the nuclear process, ${{}_{6}C}^{11}\to {{}_{5}B}^{11}+{\beta }^{+}+X, X$ stands for _______

Two deuterons undergo nuclear fusion to form a Helium nucleus. The energy released in this process is (given binding energy per nucleon for deuteron$=\text{1.1} \mathrm{MeV}$ and for helium$=\text{7.0} \mathrm{MeV}$)

The mass of a ${}_3^7\mathrm{Li}$ nucleus is $0.042 \mathrm{u}$ less than the sum of the masses of all its nucleons. The binding energy per nucleon of  ${}_3^7\mathrm{Li}$ nucleus is nearly

Imagine that a reactor converts all the given mass into energy and that it operates at a power level of ${10}^9$ watt. The mass of the fuel consumed per hour, in the reactor, will be:
(velocity of light, $c$ is $3\times {10}^{\mathrm{8 }}\mathrm{m} {\mathrm{s}}^{-1}$)

The above is a plot of binding energy per nucleon $E_{\mathrm{b}},$ against the nuclear mass $M; \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E},$ correspond to different nuclei. Consider four reactions :

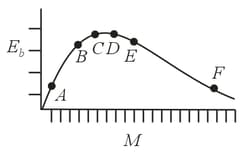
(i) $\mathrm{A}+\mathrm{B}\to \mathrm{C}+\epsilon$
(ii) $\mathrm{C}\to \mathrm{A}+\mathrm{B}+\epsilon$
(iii) $\mathrm{D}+\mathrm{E}\to \mathrm{F}+\epsilon$ and

(iv) $\mathrm{F}\to \mathrm{D}+\mathrm{E}+\epsilon$ 

where $\epsilon$ is the energy released. In which reactions $\epsilon$ positive

Four hydrogen nuclei combine to form a helium nucleus. If the mass defect in the formation of helium is $0.5\%$  and one $\mathrm{kg}$ of hydrogen undergoes fusion to form helium, the energy released in kilowatt hour is

Two deuterons undergo fusion to form a helium nucleus as ${}_1\mathrm{H}^2+{}_1\mathrm{H}^2\to {}_2\mathrm{He}^4+Q$. Given binding energy per nucleon for ${}_1\mathrm{H}^2$ and ${}_2\mathrm{He}^4$ are $1.1 \mathrm{MeV}$ and $7.00 \mathrm{MeV}$, respectively. The $Q$-value is

The voltage applied to an $X$-ray tube is $18 \mathrm{kV}.$ The maximum equivalent mass of photon emitted by the $X$-ray tube will be:

The difference between the mass of a ${}_6{}^{12}\mathrm{C}$ nucleus and the sum of the masses of the individual nucleons is $0.1 \mathrm{u}.$ Which of the following is approximately the binding energy of the nucleus?

A star consist of deuterons. It initially has ${10}^{40}$ deutrons. It produces energy by the processes

${}_{1}H^2+{}_{1}H^2⟶{}_{1}H^3+p$
${}_{1}H^2+{}_{1}H^3⟶{}_{2}H{e}^4+n$
If the average power radiated by the star is $1.6$ $\times {10}^{16}$ watt and masses of nuclei are

$M\left({}_{1}H^2\right)=3AMU, M\left(P\right)\cong M\left(n\right)\cong 1 AMU,$
$M\left({}_{2}H{e}^4\right)=4$$AMU$ and use approximation,
energy equivalent to $1AMU\cong 1000MeV$. Find the time in which the supply of deuteron in the star is exhausted.

A star has a supply of ${10}^{50}$ deuterons. It produces energy via a fusion reaction

${}_1{}^2\mathrm{H}+{}_1{}^2\mathrm{H}⟶{}_1{}^3\mathrm{H}+p$

and ${}_1{}^2\mathrm{H}+{}_1{}^3\mathrm{H}⟶{}_2{}^4\mathrm{He}+n$

where masses of nuclei are

$m\left({}^2\mathrm{H}\right)=2.014 \mathrm{amu}, m\left(p\right)=1.007 \mathrm{amu},$

$m\left(n\right)=1.008 \mathrm{amu}$ and $m\left({}^4\mathrm{He}\right)=4.001 \mathrm{amu}$

If the average power radiated by the star is ${10}^{16} \mathrm{W}$. The deuteron supply of the star is exhausted in a time of the order of $(1 \mathrm{amu}=931 \mathrm{MeV})$

The mass of deuteron $\left({}_1{\mathrm{H}}^2\right)$ nucleus is $2.0159403 \mathrm{u}.$ If the masses of proton and neutron are $1.007275 \mathrm{u}$ and $1.008667 \mathrm{u}$ respectively, calculate the binding energy per nucleon.

Binding energy of a nucleus is,