Energy Stored in a Capacitor

A capacitor in an electronic circuit is designed to slowly discharge through an indicator lamp. It is decided that the time taken for the capacitor to discharge needs to be increased. Four changes are suggested:

(1) Connect a second capacitor in parallel with the original capacitor.

(2) Connect a second capacitor in series with the original capacitor.

(3) Connect a resistor in parallel with the lamp.

(4) Connect a resistor in series with the lamp.

Which suggestions would lead to the discharge time being increased?

A circuit contains capacitors of capacitance $500\mu \mathrm{F}$ and $2000\mu \mathrm{F}$ in series with each other and in series with a resistance of $2.5\mathrm{k}\Omega$. Calculate the time taken for the charge on the plates to fall to $5\%$ of the charge when there was a p.d. of $50 \mathrm{V}$ across the plates.

 A circuit contains capacitors of capacitance $500\mu \mathrm{F}$ and $2000\mu \mathrm{F}$ In series with each other and in series with a resistance of $2.5\mathrm{k}\Omega$.

Calculate the effective capacitance of the capacitors in series.

A second capacitor of the same value is connected in series with the first capacitor.

Discuss the effect on both the current recorded and the power dissipated in the resistor.

This is a circuit that can be used to measure the capacitance of a capacitor.

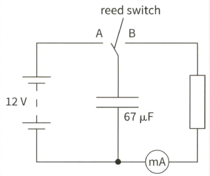
The reed switch vibrates back and forth at a frequency of $50 \mathrm{Hz}$. Each time it makes contact with A, the capacitor is charged by the battery so that there is a p.d. of $12 \mathrm{V}$ across it. Each time it makes contact with B, it is fully discharged through the resistor.

Calculate the average current in the resistor.

Figure shows two identical conducting brass spheres of radius $10 cm$ mounted on insulating stands. Sphere A has a charge of $+5.0 \times {10}^{-8} C$ and sphere B is uncharged.

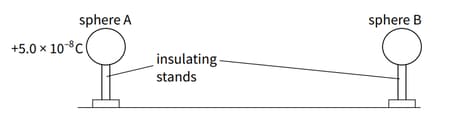
Figure shows two identical conducting brass spheres of radius $10 cm$ mounted on insulating stands. Sphere A has a charge of $+5.0 \times {10}^{-8} C$ and sphere B is uncharged.

Calculate the energy stored on each sphere.

Figure shows two identical conducting brass spheres of radius $10 cm$ mounted on insulating stands. Sphere A has a charge of $+5.0 \times {10}^{-8} C$ and sphere B is uncharged.

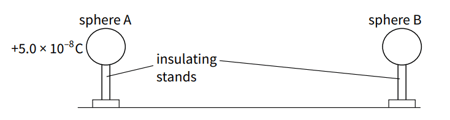
Calculate the potential at the surface of sphere A.

Show that the capacitance $\mathrm{C}$ of an isolated conducting sphere of radius $\mathrm{r}$ is given by the formula: $\mathrm{C}=4\pi {\epsilon }_0\mathrm{r}$.

Suggest why the discharge ceases while there is still some charge on the dome.

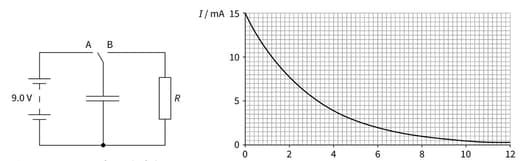
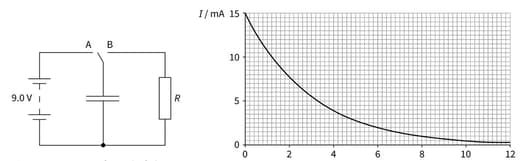
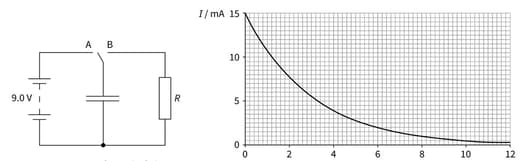
This is a circuit used to investigate the discharge of a capacitor, and a graph showing the change in current with time when the capacitor is discharged.

The charge on the capacitor is equal to the area under the graph. Estimate the charge on the capacitor when the potential difference across it is $9.0 \mathrm{V}$.

This is a circuit used to investigate the discharge of a capacitor, and a graph showing the change in current with time when the capacitor is discharged.

Explain why the current decreases as the capacitor discharges.

This is a circuit used to investigate the discharge of a capacitor, and a graph showing the change in current with time when the capacitor is discharged.

Deduce the resistance $R$ of the resistor.

(a) State one use of a capacitor in a simple electric circuit.

A $4700\mu \mathrm{F}$ capacitor has a p.d. of $12 \mathrm{V}$ across its terminals. Calculate the charge stored on the capacitor.

Given a $5000\mu \mathrm{F}$ capacitor has a p.d. of $24 \mathrm{V}$ across its plates.The capacitor is briefly connected across a bulb and half the charge flows off the capacitor. Calculate the energy dissipated in the lamp.

Given a $5000\mu \mathrm{F}$ capacitor has a p.d. of $24 \mathrm{V}$ across its plates.Calculate the energy stored on the capacitor.

A $470\mu \mathrm{F}$ capacitor is connected across the terminals of a battery of e.m.f. $9 \mathrm{V}$. Calculate the charge on the plates of the capacitor.

A capacitor has a potential difference of $6.0 \mathrm{V}$ across its plates and stores $9.0 \mathrm{mJ}$ of energy. Which row in the table gives the capacitance of the capacitor and the charge on its plates?

A $400\mu \mathrm{F}$, capacitor is charged using a $20 \mathrm{V}$, battery. It is connected across the ends of a $600\Omega$, resistor with $20 \mathrm{V}$,potential difference across its plates.

Calculate the time constant for the discharging circuit.