Gauss's Law

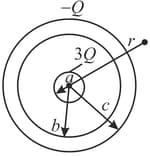
 A solid insulating sphere of radius $a$ carries a net positive charge $3Q$, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with an inner radius $b$ and outer radius $c$ and having a net charge $-Q$, as shown in the figure.

(a) Consider a spherical Gaussian surface of radius $r>c$, the net charge enclosed by this surface is _____.

(b) The direction of the electric field $r>c$ is ___ .

(c) The electric field at $r>c$ is _____.

(d) The electric field in the region with radius $r$, where $c>r>b$ , is _____.

(e) Consider a spherical Gaussian surface of radius $r$, where $c>r>b$, the net charge enclosed by this surface is _____.

(f) Consider a spherical Gaussian surface of radius $r$, where $b>r>a$, the net charge enclosed by this surface is _____.

(g) The electric field in the region $b>r>a$ is _____.

(h) Consider a spherical Gaussian surface of radius $r<a$. Find an expression for the net charge $Q\left(r\right)$ enclosed by this surface as a function of $r$. Note that the charge inside this surface is less than $3Q$.

(i) The electric field in the region $r<a$ is _____.

(j) The charge on the inner surface of the conducting shell is _____.

(k) The charge on the outer surface of the conducting shell is _____.

(l) Make a plot of the magnitude of the electric field versus $r$.

This questions has Statement $1$ and Statement $2.$ Of the four choices given after the statements, choose the one that best describes the two statements.

An insulating solid sphere of radius $R$ has a uniformly positive charge density $\rho .$ As a result of this uniform charge distribution there is a finite value of the electric potential at the centre of the sphere, at the surface of the sphere and also at a point outside the sphere. The electric potential at infinity is zero.

Statement $1$: When a charge is taken from the centre to the surface of the sphere its potential energy changes by $\frac{q\rho }{3{\epsilon }_0}$
Statement $2$: The electric field at a distance $r(r<R)$ from the centre of the sphere is $\frac{\rho r}{3{\epsilon }_0}$

In a uniformly charged sphere of total charge $Q$ and radius $R$, the electric field $E$ is plotted as function of distance from the centre. The graph which would correspond to the above will be

Let there be a spherically symmetric charge distribution with charge density varying as $\rho \left(r\right)={\rho }_0\left(\frac{5}{4}-\frac{r}{R}\right)$ up to $r=R$, and $\rho \left(r\right)=0$ for $r>R$, where $r$ is the distance from the origin. The electric field at a distance $r(r<R)$ from the origin is given by

Let $P\left(r\right)=\frac{Q}{\pi R^4}r$ be the charge density distribution for a solid sphere of radius $R$ and total charge $Q.$ For a point $p$ inside the sphere at distance $r_1$ from the centre of the sphere, the magnitude of electric field is

Consider a uniform charge distribution with charge density $2 \mathrm{C} {\mathrm{m}}^{-3}$ throughout in space. If a Gaussian sphere has a variable radius which changes at the rate of $2 \mathrm{m} {\mathrm{s}}^{-1}$, then the value of the rate of change of flux is proportional to $r^k$ ($r=$radius of the sphere). Then, find the value of $k$.

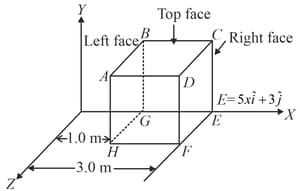
A non-uniform electric field $E=\left(5x\hat{\mathrm{i}}+3\hat{\mathrm{j}}\right) \mathrm{N} {\mathrm{C}}^{-1}$ goes through a cube of side length $2.0 \mathrm{m}.$ oriented as shown. Then,

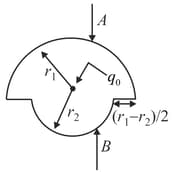
$A$ and $B$ are semi-spherical surfaces of radius $r_1$ and $r_2$ $\left(r_1>r_2\right)$ with $E_1$ and $E_2$ as the electric fields at their surfaces. Charge $q_0$ is placed as shown. What is the condition which may be satisfied?

The figure shows a neutral metallic sphere with a point charge $+Q$ placed near its surface. Electrostatic equilibrium conditions exist on the metallic sphere. Mark the correct statements.

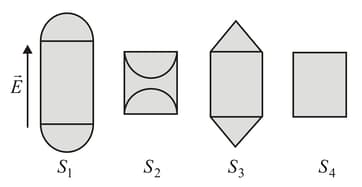
The figure shows four Gaussian surfaces consisting of identical cylindrical midsections but different end caps. The surfaces are in a uniform electric field that is directed parallel to the central axis of each cylindrical midsection. The end caps have these shapes: $S_1$, convex hemispheres; $S_2$, concave hemispheres; $S_3$, cones; $S_4$, flat disks. Rank the surfaces according to $\left(\mathrm{a}\right)$ the net electric flux through them and $\left(\mathrm{b}\right)$ the electric flux through the top end caps, the greatest first.

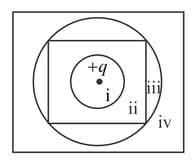
The figure shows, in cross-section, two Gaussian spheres and two Gaussian cubes that are centered on a positively charged particle. Rank greatest first, and indicate whether the magnitudes are uniform or variable along each surface.

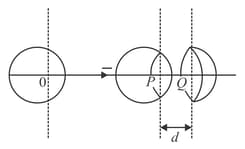
An insulating spherical shell of uniform surface charge density is cut into two parts and placed at a distance $d$ apart as shown in figure. ${\overrightarrow{E}}_P$ and ${\overrightarrow{E}}_Q$ denote the electric fields at $P$ and $Q,$ respectively. As $d$ (i.e., $PQ$)$\to \infty$

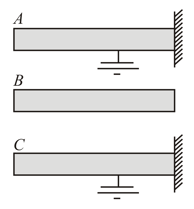
$A$, $B$ and $C$ are three large, parallel conducting plates, placed horizontally. $A$ and $C$ are rightly fixed and earthed (figure). $B$ is given some charge. Under electrostatic and gravitational forces, $B$ maybe

A thin-walled spherical conducting shell $S$ of the radius $R$ is given charge $Q$. The same amount of charge is also placed at its center $C$. Which of the following statements are correct?

The figure shows a point charge of $0.5\times {10}^{-6} \mathrm{C}$ at the centre of a spherical cavity of radius $3 \mathrm{cm}$ of a piece of metal. The electric field at,

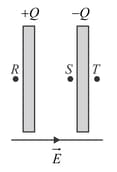
Two large thin conducting plates with a small gap in between are placed in a uniform electric field $E$ (perpendicular to the plates). The area of each plate is $A,$ and charges $+Q$ and $-Q$ are given to these plates as shown in figure. If $R, S,$ and $T$ are three points in space, then the

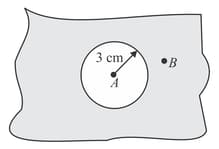
A $10 \mathrm{C}$ charge is given to a conducting spherical shell, and a $-3 \mathrm{C}$ point charge is placed inside the shell. For this arrangement, find the correct statement(s).

Consider a Gaussian spherical surface covering a dipole of charge $q$ and $-q,$ then

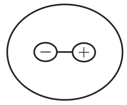
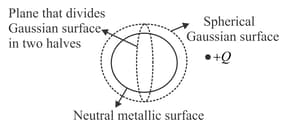
Consider Gauss's law:

$\oint \overrightarrow{E}·\overrightarrow{d}s=\frac{q}{{\epsilon }_0}$

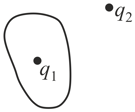
Then, for the situation shown in figure at the Gaussian surface

In an insulating medium (dielectric constant $=1$) the charge density varies with $y$-coordinate as $\rho =by$, where $b$ is a positive constant. The electric field is zero at $y=0$ and everywhere else it is along $y$-direction. Calculate the electric field as a function of $y$.