Combining Velocities

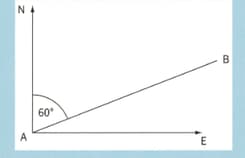
A small aircraft for one is used for a short horizontal flight. On its journey from  $\mathrm{A} \mathrm{to} \mathrm{B}$, the resultant velocity is $15 {\mathrm{ms}}^{-1}$in a direction ${60}^{°}$ east of north and the wind velocity is $7.5 {\mathrm{ms}}^{-1}$due north.

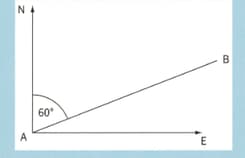
After flying $5 \mathrm{km}$from $\mathrm{A} \mathrm{to} \mathrm{B}$, the aircraft return along the same path from $\mathrm{B} \mathrm{to} \mathrm{A}$ with a resultant velocity of $13.5 {\mathrm{ms}}^{-1}$ assuming that the time spent at $\mathrm{B}$ is negligible, calculate the average speed for the complete journey from $\mathrm{A} \mathrm{to} \mathrm{B}$ and back to $\mathrm{A}$.

A small aircraft for one is used for a short horizontal flight. On its journey from  $\mathrm{A} \mathrm{to} \mathrm{B}$, the resultant velocity is $15 {\mathrm{ms}}^{-1}$in a direction ${60}^{°}$ east of north and the wind velocity is $7.5 {\mathrm{ms}}^{-1}$due north. Show that for the aircraft to travel from $\mathrm{A} \mathrm{to} \mathrm{B}$ it should point due east.

A Plane has an airspeed of $500 \mathrm{kmph}$ due north. A Wind blows at $100 \mathrm{km}/\mathrm{h}$ from east to west. Draw a vector diagram to

The plane lies for $15 \min$. Calculate the displacement of the plane in this time.

A Plane has an airspeed of $500 \mathrm{kmph}$ due north. A Wind blows at $100 \mathrm{km}/\mathrm{h}$ from east to west. Draw a vector diagram to calculate the resultant velocity of the plan Give The direction of travel of the plane with respect to north.

A river flows from west to east with a constant velocity of $1.0 m{s}^{-1}$. A boat leaves the south bank heading due north at $2.4 m{s}^{-1}$. Find the resultant velocity of the boat.

A vector $\mathbf{P}$ of magnitude $3.0 \mathrm{N}$  acts towards the right and a vector $\mathbf{Q}$ of magnitude$4.0 \mathrm{N}$ acts upwards. What is the magnitude and direction of the vector $(P-Q)$?

Which of the following pairs contains one vector and one scalar quantity?

A velocity of $5.0 {\mathrm{ms}}^{-1}$ is due north.  Subtract from it another velocity that is $5.0 {\mathrm{ms}}^{-1}$ due west.  Subtract from it another velocity that is $5.0 {\mathrm{ms}}^{-1}$ due east.

A velocity of $5.0 {\mathrm{ms}}^{-1}$ is due north.  Subtract from it another velocity that is $5.0 {\mathrm{ms}}^{-1}$ due west.

A velocity of $5.0 {\mathrm{ms}}^{-1}$ is due north.  Substrata from it another velocity that is $5.0 {\mathrm{ms}}^{-1}$ due north.

A velocity of $5.0 {\mathrm{ms}}^{-1}$ is due north.  Subtract from it another velocity that is $5.0 {\mathrm{ms}}^{-1}$ due south.

A stone is thrown from a cliff and strike the surface of the sea with a vertical velocity of $18 {\mathrm{ms}}^{-1}$ and a horizontal velocity $v$. The resultant of these two velocities is $25 {\mathrm{ms}}^{-1}$. Draw a vector diagram showing the two velocities and the resultant. Use your diagram to find the angle between the stone and the vertical as it strikes the water.

A stone is thrown from a cliff and strike the surface of the sea with a vertical velocity of $18 {\mathrm{ms}}^{-1}$ and a horizontal velocity $v$. The resultant of these two velocities is $25 {\mathrm{ms}}^{-1}$. Draw a vector diagram showing the two velocities and the resultant. Use your diagram to find the value of $\mathrm{v}$.