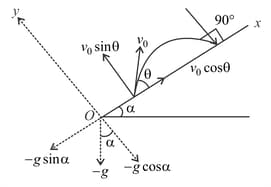
Projectile Motion on an Inclined Plane

The windscreens of two motorcars are having slopes $30°$ and $15°$ respectively. At what ratio $\frac{v_1}{v_2}$ of the velocities of cars will their drivers see the hailstones bounced by windscreen of their cars in the vertical direction? Assume hailstones are falling vertically.

A ball is projected horizontally from an incline to strike a cart sliding on the incline. Neglect height of cart and point of projection of ball above incline. At the instance the ball is thrown, the speed of the cart is $v$ (in $\mathrm{m} {\mathrm{s}}^{-1}$). Find $v$ so that the ball strikes the cart.

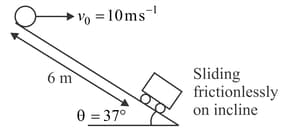
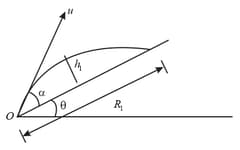
In figure, find the horizontal velocity $u$ (in $\mathrm{m} {\mathrm{s}}^{-1}$) of a projectile so that it hits the inclined plane perpendicularly. Given $H=6.25 \mathrm{m}$.

A particle is projected up an inclined plane of inclination $\beta$ at an elevation $\alpha$ to the horizontal. Find the ratio between $\tan \alpha$ and $\tan \beta ,$ if the particle strikes the plane horizontally.

A body has maximum range $R_1$ when projected up the plane. The same body when projected down the inclined plane, it has maximum range $R_2$. Find the maximum horizontal range. Assume that equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.

An inclined plane makes an angle ${\mathrm{\theta }}_0=30°$ with the horizontal. A particle is projected from this plane with a speed of $5{ \mathrm{m} \mathrm{s}}^{-1}$ at an angle of elevation $\beta =30°$ with the horizontal as shown in the figure.

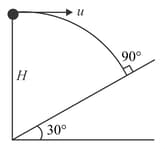
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for $\beta =120°$.

A body is projected up with a speed $v_0$ along the line of greatest slope of an inclined plane of angle of inclination $\beta$. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.

At what angle should a ball be projected up an inclined plane with a velocity $v_0$ so that it may hit the incline normally. The angle of the inclined plane with the horizontal is $\alpha$.

A mango in a tree is located at a horizontal and vertical distance of $30 \mathrm{m}$ and $40 \mathrm{m}$, respectively, from the point of projection of a stone. Find the minimum speed and the critical angle of projection of the stone so as to hit the mango.

A body is thrown at an angle ${\theta }_0$ with the horizontal such that it attains a speed equal to $\sqrt{\frac{2}{3}}$ times the speed of projection when the body is at half of its maximum height. Find the angle ${\theta }_0$.

A truck starts from origin accelerating with $a{ \mathrm{m} \mathrm{s}}^{-2}$ in positive $x$-axis direction. After $2 \mathrm{s}$, a man standing at the starting point of the truck projected a ball at an angle $30°$ with velocity $v$ $\mathrm{m} {\mathrm{s}}^{-1}$. Find the relation between $a$ and $v$ such that the ball hits the truck. (Assume that truck is moving on horizontal plane and the man projected the ball from the same horizontal level of truck).

Two inclined planes $OA$ and $OB$ having inclination (with horizontal) $30°$ and $60°$, respectively, intersect each other at $O$ as shown in the figure. A particle is projected from point $P$ with velocity $u=10\sqrt{3} \mathrm{m}{ \mathrm{s}}^{-1}$ along a direction perpendicular to plane $OA$. If the particle strikes plane $OB$ perpendicularly at $Q$, calculate the

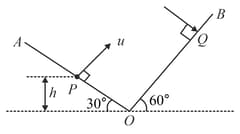
(a) velocity with which the particle strikes the plane $OB$.
(b) time of flight.
(c) vertical height $h$ of $P$ from $O$.
(d) maximum height from $O$, attained by the particle.
(e) distance $PQ$.

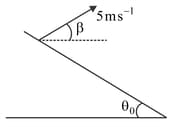
Two balls are thrown from an inclined plane at an angle of projection $\alpha$ with the plane one up the inclined plane and the other down the incline as shown in the figure. If $R_1$, and $R_2$ be their respective ranges, then

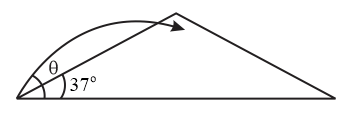
A shot is fired at an angle $\mathrm{\theta }$ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of the projection $\mathrm{\theta }$.

A particle is thrown at time $t=0$ with a velocity of $10 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle $60°$ with the horizontal from a point on an inclined plane, making an angle of $30°$ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is

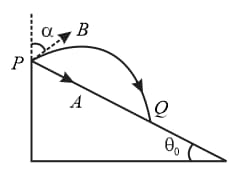
figure shows that particle $A$ is projected from point $P$. with velocity $u$ along the plane and simultaneously another particle $B$ with velocity $v$ at an angle $\alpha$ with vertical. The particles collide at point $Q$ on the plane. Then

The maximum range of a projectile is $500 \mathrm{m}$. If the particle is thrown up a plane which is inclined at an angle of $30°$ with the same speed, the distance covered by it along the inclined plane will be,

A projectile is fired with a velocity $v$ at right angle to the slope inclined at an angle $\mathrm{\theta }$ with the horizontal. The range of the projectile along the inclined plane is

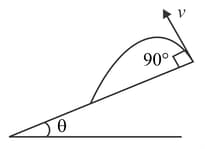
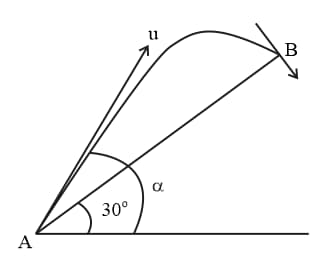
In the figure, the time taken by the projectile to reach from $A$ to $B$ is $t$. Then the distance $AB$ is equal to
  

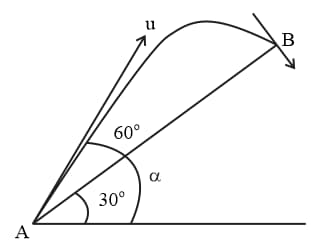
A particle is projected with a certain velocity at an angle above the horizontal from the foot of an inclined plane of inclination $30°$. If the particle strikes the plane normally, then $\alpha$ is equal to