Projectile Motion

A ball is projected at an angle $\mathrm{\theta }.$ As the ball flies through the air, the observer at the point of projection, follows it with his eyes. When it reaches maximum height $Y,$ his eyes are directed at an angle $\mathrm{\varphi }$ with respect to the horizontal. What is the value of $\frac{\tan \left(\mathrm{\theta }\right)}{\tan \left(\mathrm{\varphi }\right)}?$

A projectile is launched at time $t=0$ from point $A$ which is at height $1 \mathrm{m}$ above the floor with speed $v \mathrm{m} {\mathrm{s}}^{-1}$ and at an angle $\theta =45°$ with the floor. It passes through a hoop at $B$ which is $1 \mathrm{m}$ above $A$ and $B$ is the highest point of the trajectory. The horizontal distance between $A$ and $B$ is $d$ meters. The projectile then falls into a basket, hitting the floor at $C$ a horizontal distance $3d$ meters from $A.$ Find $l$ (in m).

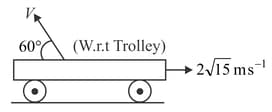
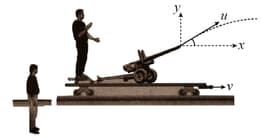
A particle is projected from a stationary trolley. After projection, the trolley moves with a velocity $2\sqrt{15} \mathrm{m} {\mathrm{s}}^{-1}.$ For an observer on the trolley, the direction of the particle is as shown in .the figure while for the observer on the ground, the ball rises vertically. The maximum height reached by the ball from the trolley is $h$ meter. The value of $h$ will be ______.

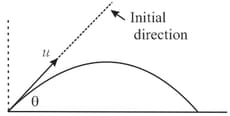
A ball is projected from the origin. The $x$- and $y$-coordinates of its displacement are given by $x=3t$ and $y=4t-5t^2.$ Find the velocity of projection (in ${\mathrm{ms}}^{-1}$).

A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of $1 \mathrm{m} {\mathrm{s}}^{-2}$ and the projection velocity in the vertical direction is $9.8 \mathrm{m} {\mathrm{s}}^{-1}$. How far behind the boy will the ball fall on the car? (in meters)

A body is thrown with the velocity $v_0$ at an angle of $\theta$ to the horizon. Determine $v_0$ in $\mathrm{m} {\mathrm{s}}^{-1}$ if the maximum height attained by the body is $5 \mathrm{m}$ and at the highest point of its trajectory, the radius of curvature is $r=3 \mathrm{m}$. Neglect air resistance. [Use $\sqrt{80}$ as $9$.]

A particle is projected from the ground at an angle $30°$ with the horizontal with an initial speed $20{ \mathrm{m} \mathrm{s}}^{-1}.$ After how much time [in a second] will the velocity vector of projectile be perpendicular to the initial velocity?

A particle is projected with velocity $u$ at angle $\mathrm{\theta }$ with horizontal. Calculate the time when it is moving perpendicular to initial direction. Also calculate the velocity at this position.

A man is sitting in an open car which is travelling along a road at a speed of $30 \mathrm{m}{ \mathrm{s}}^{-1}$. The man stands up and throws a ball at a speed of $15 \mathrm{m}{ \mathrm{s}}^{-1}$ relative to himself at an angle $\mathrm{\theta }$ to the horizontal. The moment the man throws the ball, the driver of the car begins to accelerate at a constant rate of $10\sqrt{3} \mathrm{m}{ \mathrm{s}}^{-2}$, in the direction in which it was initially travelling.
(a) Find the value of $\mathrm{\theta }$ if the man in the car catches the ball.
(b) Find the time at which the man catches the ball if the instant at which the ball was thrown is $t=0$.

Assume that the time at which the ball travels contains the line of the motion of the car and that $g=10 \mathrm{m}{ \mathrm{s}}^{-2}$.

A man is standing on a rail road car travelling with a constant speed of $v=10{ \mathrm{m} \mathrm{s}}^{-1}$ (figure). He wishes to throw a ball through a stationary hoop $5 \mathrm{m}$ above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of $12.5{ \mathrm{m} \mathrm{s}}^{-1}$ with respect to himself.

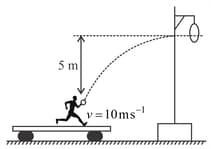
(a) What must be the vertical component of the initial velocity of the ball?
(b) How many seconds after he releases the ball will it pass through the hoop?
(c) At what horizontal distance in front of the loop must he release the ball?

A shell is projected from a gun with a muzzle velocity, $u$. The gun is fitted with a trolley car at an angle $\theta$ as shown in the figure. If the trolley car is made to move with constant velocity $y$ towards right, find the
(a) horizontal range of the shell relative to ground.
(b) horizontal range of the shell relative to a person travelling with trolley.

A boy of height $1.5 \mathrm{m}$, making move on a skateboard due east with velocity $4 \mathrm{m}{ \mathrm{s}}^{-1}$, throws a coin vertically up with a velocity of $3 \mathrm{m}{ \mathrm{s}}^{-1}$ relative to himself.
(a) Find the total displacement of the coin relative to the ground till it comes to the hand of the boy.
(b) What is the maximum height attained by the coin w.r.t to ground?

A boy throws a ball in air at $60°$ to the horizontal along a road with a speed of $10{ \mathrm{m} \mathrm{s}}^{-1}$. Another boy sitting in a passing car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if the car has a speed of $5{ \mathrm{m} \mathrm{s}}^{-1}$. Give explanation to support your diagram.

A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.

A particle projected at a definite angle $\alpha$ to the horizontal passes through points $(a, b)$ and $(b, a)$, referred to horizontal and vertical axes through the point of projection. Show that:
(a) The horizontal range $R=\frac{a^2+ab+b^2}{a+b}$
(b) The angle of projection $\alpha$ is given by ${\tan }^{-1}\left[\frac{a^2+ab+b^2}{ab}\right]$.

A particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If $a$ and $b$ are the base angles of the triangle and $\theta$ the angle of projection, prove that $\mathrm{tan\theta }=$$\tan \alpha +\tan \beta$.

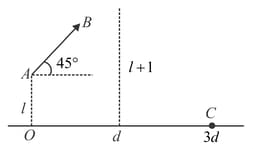
From a point on the ground at a distance $a$ from the foot of a pole, a ball is thrown at an angle of $45°$ which just touches the top of the pole and strikes the ground at a distance of $b$, on the other side of it. Find the height of the pole.

A particle is projected from the ground at $t=0$, so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity $u$ and at angle $\mathrm{\theta }$ with the horizontal, if the particle passes just grazing top of the wall at time $t=t_1$ and $t=t_2$, then calculate
(a) the height of the wall.
(b) the time $t_1$ and $t_2$ in terms of height of the wall.
(c) Write the expression for calculating the range of this projectile and separation between the walls.

A jet of water is projected at an angle $\mathrm{\theta }=45°$ with horizontal from point $A$ which is situated at a distance $x=OA=$ (a) $1/2$ $\mathrm{m}$, (b) $2 \mathrm{m}$ from a vertical wall. If the speed of projection is $v_0=\sqrt{10}{ \mathrm{m} \mathrm{s}}^{-1}$, find point $P$ of striking of the water jet with the vertical wall.

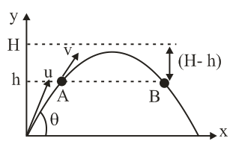
The figure shows two positions $A$ and $B$ at the same height $h$ above the ground. If the maximum height of the projectile is $H$, then determine the time $t$ elapsed between the positions $A$ and $B$ in terms of $H$ and $h$.